题目内容
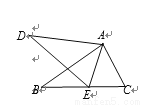
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C, D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比为3∶2.
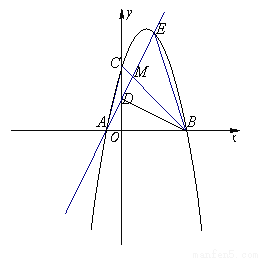
(1)求这条抛物线对应的函数关系式;
(2)连结BD,试判断BD与AD的位置关系,并说明理由;
(3)连结BC交直线AD于点M,在直线AD上,是否存在这样的点N(不与点M重合),使得以A、B、N为顶点的三角形与△ABM相似?若存在,请求出点N的坐标;若不存在,请说明理由.
(1)根据△ABE与△ABC的面积之比为3∶2及E(2,6),可得C(0,4). ∴D(0,2). 由D(0,2)、E(2,6)可得直线AD所对应的函数关系式为y=2x+2. 当y=0时,2x+2=0,解得x=-1. ∴A(-1,0). 由A(-1,0)、C(0,4)、E(2,6)求得抛物线对应的函数关系式为 y=-x2+3x+4. (2)BD⊥AD. 求得B(...
练习册系列答案
相关题目
二次函数y=ax2+bx+c的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
二次函数图象的对称轴是( )
A. 直线x=1 B. y轴 C. 直线x=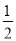 D. 直线x=﹣
D. 直线x=﹣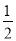


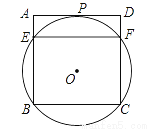
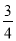 ,DF=
,DF=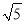 ,求EF的长.
,求EF的长.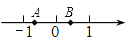
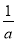 D.
D. 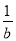
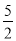 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.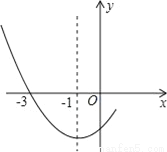
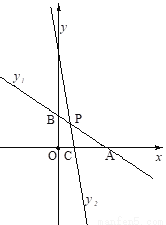
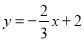 与x轴、y轴分别相交于点A和点B,直线
与x轴、y轴分别相交于点A和点B,直线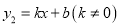 经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.