��Ŀ����
��ͼ����������ABCD����B��C�ġ�O��AD�����ڵ�P����AB��CD�ֱ��ཻ�ڵ�E��F������EF��
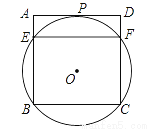
��1����֤��PFƽ�֡�BFD��
��2����tan��FBC= 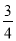 ��DF=
��DF=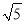 ����EF�ij���
����EF�ij���
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����������ABCD����B��C�ġ�O��AD�����ڵ�P����AB��CD�ֱ��ཻ�ڵ�E��F������EF��

��1����֤��PFƽ�֡�BFD��
��2����tan��FBC= 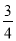 ��DF=
��DF=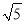 ����EF�ij���
����EF�ij���