题目内容
数轴上的点M对应的数是-4,一只蚂蚁从M点出发沿数轴以每秒2个单位长度的速度爬行,当它到达数轴上的N点后,立即返回到原点,共用11秒.
(1)蚂蚁爬行的路程是多少?
(2)点N对应的数是多少?
(3)点M和点N之间的距离是多少?
(1)蚂蚁爬行的路程是多少?
(2)点N对应的数是多少?
(3)点M和点N之间的距离是多少?
考点:数轴
专题:
分析:(1)根据公式:路程=速度×时间,直接得出答案;
(2)先设点N表示的数为a,分两种情况:点M在点N左侧或右侧,求出从M点到N点单位长度的个数,再由M点表示的数是-4,从点N返回到原点即可得出N点表示的数.
(3)根据点N表示的数即可得出点M和点N之间的距离.
(2)先设点N表示的数为a,分两种情况:点M在点N左侧或右侧,求出从M点到N点单位长度的个数,再由M点表示的数是-4,从点N返回到原点即可得出N点表示的数.
(3)根据点N表示的数即可得出点M和点N之间的距离.
解答:解:(1)2×11=22(个单位长度).
故蚂蚁爬行的路程是22个单位长度.
(2)①当点M在点N左侧时:
a+4+a=22,
a=9;
②当点M在点N右侧时:
-a-4-a=22,
a=-13;
(3)点M和点N之间的距离是13或9.
故蚂蚁爬行的路程是22个单位长度.
(2)①当点M在点N左侧时:
a+4+a=22,
a=9;
②当点M在点N右侧时:
-a-4-a=22,
a=-13;
(3)点M和点N之间的距离是13或9.
点评:本题考查了数轴,两点之间距离的求法:右边的数减去左边的数.

练习册系列答案
相关题目
两个多边形相似,一组对应边的长分别为3cm和2cm,若它们的面积之差为7cm2,则较大的多边形的面积是( )
| A、14cm2 |
| B、21cm2 |
| C、5.6cm2 |
| D、12.6cm2 |
 如图,矩形ABCD中,点A的坐标是(-3,1),点C的纵坐标是7,则点C的横坐标为
如图,矩形ABCD中,点A的坐标是(-3,1),点C的纵坐标是7,则点C的横坐标为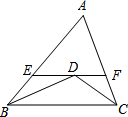 如图,在△ABC中,AB=8,BC=6,AC=5,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,则△AEF的周长等于( )
如图,在△ABC中,AB=8,BC=6,AC=5,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,则△AEF的周长等于( )