题目内容
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )| A、60° | B、75° |
| C、90° | D、85° |
考点:旋转的性质
专题:
分析:如图,运用旋转变换的性质得到:∠BAC=∠DAE,∠D=∠B;求出∠B,运用三角形的内角和定理即可解决问题.
解答: 解:如图,由题意得:∠BAC=∠DAE,∠D=∠B;
解:如图,由题意得:∠BAC=∠DAE,∠D=∠B;
∴∠BAD=∠CAE=65°;
∵AD⊥BC,
∴∠B=90°-∠BAC=25°,∠D=25°,
∴∠DAE=180°-25°-70°=85°,
∴∠BAC=85°,
故选D.
 解:如图,由题意得:∠BAC=∠DAE,∠D=∠B;
解:如图,由题意得:∠BAC=∠DAE,∠D=∠B;∴∠BAD=∠CAE=65°;
∵AD⊥BC,
∴∠B=90°-∠BAC=25°,∠D=25°,
∴∠DAE=180°-25°-70°=85°,
∴∠BAC=85°,
故选D.
点评:该题主要考查了旋转变换的性质、三角形的内角和定理及其应用问题;准确找出图形中隐含的相等的角或边是解题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、4a2b-3a2b=1 |
| B、4a2b×3a2b=12a4b2 |
| C、(2a2)3=6a6 |
| D、(a+b)2=a2+b2 |
中国是仅次于美国的世界第二大经济体.国家统计局发布的《2013年国民经济和社会发展统计公报》显示2013年我国国内生产总值为56.89万亿元,同比增长7.7%,56.89万亿元用科学记数法表示为( )
| A、5.689×106亿元 |
| B、0.5689×106亿元 |
| C、5.689×105亿元 |
| D、5689×102亿元 |
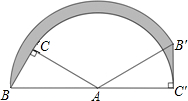 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至A′B′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至A′B′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
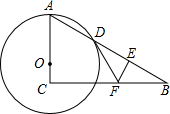 如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.
如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.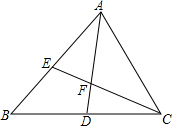 如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证:
如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证: 如图,以O为顶点的角有
如图,以O为顶点的角有 如图,△ABC中,BO、CO分别平分∠ABC和∠ACB,过点O平行于BC的直线分别交AB、AC于点D、E,已知AB=9cm,AC=8cm,求△ADE的周长.
如图,△ABC中,BO、CO分别平分∠ABC和∠ACB,过点O平行于BC的直线分别交AB、AC于点D、E,已知AB=9cm,AC=8cm,求△ADE的周长.