题目内容
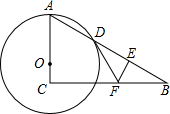 如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.
如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.(1)连结DF,请你判断直线DF与⊙O的位置关系,并证明你的结论;
(2)当点O运动到OA=2OC时,恰好有点D是AE的中点,求tan∠B(∠B=30°).
考点:切线的判定
专题:计算题
分析:(1)连结OD,如图,根据线段垂直平分线的性质得FB=FD,则∠B=∠FDB,而∠A=∠ODA,利用∠B+∠A=90°,即可得到∠ODA+∠FDB=90°,可判断OD⊥DF,于是根据切线的判断定理得到DF为⊙O的切线;
(2)先通过计算得到
=
,而∠A公共,则可判断△AOE∽△ACB,所以∠AOE=∠C=90°,则可判断OD为直角三角形AOE斜边上的中线,得到OD=AD,于是可证明△AOD为等边三角形,所以∠A=60°,则∠B=30°,然后利用特殊角的三角函数值求解.
(2)先通过计算得到
| AO |
| AC |
| AE |
| AB |
解答:解:(1)直线DF与⊙O相切.理由如下:
连结OD,如图,
∵DB垂直平分线交BC于F,
∴FB=FD,
∴∠B=∠FDB,
∵OA=OD,
∴∠A=∠ODA,
∵∠C=90°,
∴∠B+∠A=90°,
∴∠ODA+∠FDB=90°,
∴∠ODF=90°,
∴OD⊥DF,
∴DF为⊙O的切线;
(2)连结OE,如图,
∵OA=2OC,
∴
=
,
∵点D是AE的中点,
∴AD=DE,
而DE=DE,
∴
=
,
∴
=
,
而∠A公共,
∴△AOE∽△ACB,
∴∠AOE=∠C=90°,
∴OD为直角三角形AOE斜边上的中线,
∴OD=AD,
而OA=OD,
∴△AOD为等边三角形,
∴∠A=60°,
∴∠B=30°,
∴tanB=tan30°=
.
连结OD,如图,
∵DB垂直平分线交BC于F,
∴FB=FD,
∴∠B=∠FDB,
∵OA=OD,
∴∠A=∠ODA,
∵∠C=90°,
∴∠B+∠A=90°,
∴∠ODA+∠FDB=90°,
∴∠ODF=90°,
∴OD⊥DF,

∴DF为⊙O的切线;
(2)连结OE,如图,
∵OA=2OC,
∴
| AO |
| AC |
| 2 |
| 3 |
∵点D是AE的中点,
∴AD=DE,
而DE=DE,
∴
| AE |
| AB |
| 2 |
| 3 |
∴
| AO |
| AC |
| AE |
| AB |
而∠A公共,
∴△AOE∽△ACB,
∴∠AOE=∠C=90°,
∴OD为直角三角形AOE斜边上的中线,
∴OD=AD,
而OA=OD,
∴△AOD为等边三角形,
∴∠A=60°,
∴∠B=30°,
∴tanB=tan30°=
| ||
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )| A、60° | B、75° |
| C、90° | D、85° |
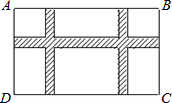 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,若通道的宽设计成xm,则阴影部分的面积是
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,若通道的宽设计成xm,则阴影部分的面积是
 如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x.
如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x. 如图,AB是⊙O的直径,C是圆上一点,过点C作CD⊥AB于点D,延长CD交圆于点E,过点C作AE的平行线交圆于点F,连接EF,交AB于H,AC,EF的延长线相较于G
如图,AB是⊙O的直径,C是圆上一点,过点C作CD⊥AB于点D,延长CD交圆于点E,过点C作AE的平行线交圆于点F,连接EF,交AB于H,AC,EF的延长线相较于G 如图,点O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠OAE的度数.
如图,点O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠OAE的度数.