Question

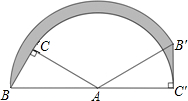如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至A′B′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为（　　）

• A、

  5

  6

  π
• B、

  7

  6

  π
• C、

  5

  12

  π
• D、

  7

  12

  π

Answer 1

考点：扇形面积的计算,旋转的性质

专题：

分析：先根据Rt△ABC中，∠C=90°，∠BAC=30°，AB=2求出BC及AC的长，再根据题意得出S_阴影=AB扫过的扇形面积-AC扫过的扇形面积．

解答：解：∵Rt△ABC中，∠C=90°，∠BAC=30°，AB=2，
∴BC=

1

2

AB=

1

2

×2=1，AC=2×

3

2

=

3

，
∴∠BAB′=150°，
∴S_阴影=AB扫过的扇形面积-AC扫过的扇形面积=

150π×22

360

-

150π×( 3 )2

360

=

5π

12

．
故选C．

点评：本题考查的是扇形的面积公式，根据题意得出S_阴影=AB扫过的扇形面积-AC扫过的扇形面积是解答此题的关键．