题目内容
8.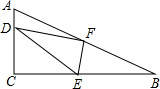 在Rt△ABC中,F是斜边AB的中点,D、E分别在边CA、CB上,满足∠DFE=90°.若AD=8,BE=4.求线段DE的长度?
在Rt△ABC中,F是斜边AB的中点,D、E分别在边CA、CB上,满足∠DFE=90°.若AD=8,BE=4.求线段DE的长度?
分析 根据题意把△ACB绕点F旋转180°后,得到△BMA,得到四边形ACBM为矩形,分别延长EF和DF,与AM交于G,与MB交于交于H,连接DG,GH,HE,DE,得到四边形DEHG为菱形,根据勾股定理计算即可.
解答 解: 根据题意把△ACB绕点F旋转180°后,得到△BMA,得到四边形ACBM为矩形,
根据题意把△ACB绕点F旋转180°后,得到△BMA,得到四边形ACBM为矩形,
分别延长EF和DF,与AM交于G,与MB交于交于H,连接DG,GH,HE,DE,
∵∠AFD=∠BFH,AF=FB,∠ADF=∠BHF,
∴△ADF≌△BHF,
∴DF=HF,
同理证明△AFG≌△BFE,得到GF=EF,且DH⊥GE,
∴四边形DEHG为菱形,
∴DE=DG=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$.
点评 本题考查的是直角三角形的性质,在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
18.一次函数y=-2x+3的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
19.如果一个多边形的内角和是它的外角和的n倍,则这个多边形的边数是( )
| A. | n | B. | 2n-2 | C. | 2n | D. | 2n+2 |
16.下列各式成立的是( )
| A. | -1>0 | B. | 3>-2 | C. | -2<-5 | D. | 1<-2 |
3.菱形和矩形都具有的性质是( )
| A. | 对角线互相垂直 | B. | 对角线相等 | C. | 对角线互相平分 | D. | 对角线平分对角 |
13.(-$\frac{3}{2}$)2006•($\frac{2}{3}$)2007的计算结果是( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
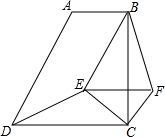 如图,直角梯形ABCD中,AB∥CD,∠DCB=90°,AB=5,BC=10,tan∠ADC=2.
如图,直角梯形ABCD中,AB∥CD,∠DCB=90°,AB=5,BC=10,tan∠ADC=2.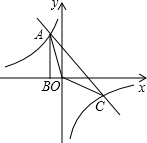 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.