题目内容
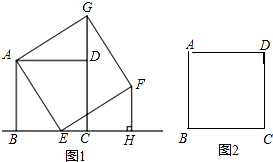
如图1,在正方形ABCD中,E是BC边上的动点(点E不与端点B、C重合),以AE为边,在直线BC的上方作矩形AEFG.使顶点G恰好落在射线CD上,过点F作FH⊥BC,交BC的延长线于点H.
(1)求证:①矩形AEFG是正方形;②BE=HC;
(2)若题设中动点E在BC的延长线上,其他条件不变,请在图2中补全图形,猜想(1)中的两个结论是否成立,请直接写出结论,不需要证明.
(1)求证:①矩形AEFG是正方形;②BE=HC;
(2)若题设中动点E在BC的延长线上,其他条件不变,请在图2中补全图形,猜想(1)中的两个结论是否成立,请直接写出结论,不需要证明.

考点:全等三角形的判定与性质,正方形的判定与性质
专题:
分析:(1)①证明△ABE≌△ADG,即可解决问题.
②证明△AEB≌△EFH,得到AB=EH,借助AB=BC,即可解决问题.
(2)补全图2如图所示,(1)中的两个结论仍然成立.
②证明△AEB≌△EFH,得到AB=EH,借助AB=BC,即可解决问题.
(2)补全图2如图所示,(1)中的两个结论仍然成立.
解答:解: (1)证明:①∵四边形ABCD是正方形,
(1)证明:①∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADC
=∠ADG=90°;
∵四边形AEFG是矩形,
∴∠EAG=90°,
∴∠BAD=∠EAG=90°.
∴∠BAD-∠EAD=∠EAG-∠EAD,
即∠BAE=∠DAG;
在△ABE与△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG.
∴矩形AEFG是正方形.
②∵矩形AEFG是正方形,
∴AE=EF,∠AEF=90°,
∴∠AEB+∠FEH=90°;
又∵∠AEB+∠EAB=90°,
∴∠EAB=∠FEH.
在△AEB与△EFH中,
,
∴△AEB≌△EFH(AAS),
∴AB=EH.
∵AB=BC,
∴BC=EH.
∵BC=BE+EC,EH=HC+EC,
∴BE=HC.
(2)补全图2如图所示:(1)中的两个结论仍然成立.
 (1)证明:①∵四边形ABCD是正方形,
(1)证明:①∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADC
=∠ADG=90°;
∵四边形AEFG是矩形,
∴∠EAG=90°,
∴∠BAD=∠EAG=90°.
∴∠BAD-∠EAD=∠EAG-∠EAD,
即∠BAE=∠DAG;
在△ABE与△ADG中,
|
∴△ABE≌△ADG(SAS),
∴AE=AG.
∴矩形AEFG是正方形.
②∵矩形AEFG是正方形,
∴AE=EF,∠AEF=90°,
∴∠AEB+∠FEH=90°;
又∵∠AEB+∠EAB=90°,
∴∠EAB=∠FEH.
在△AEB与△EFH中,
|
∴△AEB≌△EFH(AAS),
∴AB=EH.
∵AB=BC,
∴BC=EH.
∵BC=BE+EC,EH=HC+EC,
∴BE=HC.
(2)补全图2如图所示:(1)中的两个结论仍然成立.
点评:该题以正方形为载体,以考查正方形的性质、全等三角形的判定及其性质的应用为核心构造而成;牢固掌握正方形的性质、全等三角形的判定及其性质是灵活运用的基础和关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
| A、1cm |
| B、7cm |
| C、3cm或4cm |
| D、1cm或7cm |
若二次根式
有意义,则x的取值范围为( )
| 1+2x |
A、x≥-
| ||
B、x≤-
| ||
C、x≥
| ||
D、x≤
|
下列各组数中互为相反数的是( )
| A、(-2)3与-23 | ||
B、2与
| ||
| C、-1与(-1)2 | ||
| D、2与|-2| |
 如图,AB为⊙O的直径,弦CD⊥AB于点E,∠C=25°,AB=6,则劣弧
如图,AB为⊙O的直径,弦CD⊥AB于点E,∠C=25°,AB=6,则劣弧 |
| CD |
| A、10π | ||
B、
| ||
C、
| ||
D、
|
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |