题目内容
20.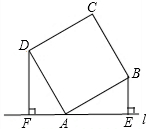 如图,直线l过正方形ABCD的顶点A,BE⊥l于点E,DF⊥l于点F,若BE=2,DF=4,则EF的长为( )
如图,直线l过正方形ABCD的顶点A,BE⊥l于点E,DF⊥l于点F,若BE=2,DF=4,则EF的长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 6 | D. | 8 |
分析 通过证明△ABE≌△DAF,得AE=DF,AF=BE,进而求出EF.
解答 解:∵正方形ABCD,
∴AD=AB, ∠DAB=90°,
∠DAB=90°,
∵BE⊥l于点E,DF⊥l于点F,
∴∠AFD=∠AEB=90°,
∴∠FAD+∠FDA=90°,且∠EAB+∠FAD=90°,
∴∠FDA=∠EAB,
在△ABE和△ADF中
∵$\left\{\begin{array}{l}{∠AFD=∠AEB}\\{∠FDA=∠EAB}\\{AD=AB}\end{array}\right.$,
∴△ABE≌△DAF(AAS),
即AE=DF=2,AF=BE=4,
∴EF=AE+AF=4+2=6,
故选C.
点评 本题考查了正方形的性质以及全等三角形的判定和勾股定理等知识,解本题的关键是证明△ABE≌△DAF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某商场自今年二月份起销售额连续增长,二月份和三月份的平均增长率为a%,则三月份的销售额比一月份增长了( )
| A. | 2a% | B. | 1+2a% | C. | (2+a%)a% | D. | (1+a%)2 |
15.$\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$,$\frac{7}{16}$,$\frac{11}{32}$,( )
| A. | $\frac{15}{64}$ | B. | $\frac{1}{4}$ | C. | $\frac{13}{48}$ | D. | $\frac{1}{3}$ |
5.下列说法错误的是( )
| A. | $\sqrt{3}$是3的平方根 | B. | |$\sqrt{2}$-1|=$\sqrt{2}$-1 | ||
| C. | -$\sqrt{5}$的相反数是$\sqrt{5}$ | D. | 带根号的数都是无理数 |
 如图,正方形ABCD和CEFG的边长分别为m、n,试用m、n的代数式表示三角形BDF的面积S.
如图,正方形ABCD和CEFG的边长分别为m、n,试用m、n的代数式表示三角形BDF的面积S.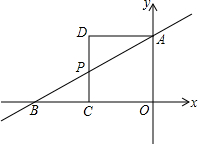 如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2-12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.
如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2-12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.