题目内容
4.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元,每个月的销售利润为y元,那么涨价后:(1)每件商品的售价可以表示为50+x.
(2)每件商品的利润可以表示为10+x.
(3)销量可以表示为210-10x.
(4)每个月的销售利润为y=-10x2+110x+2100.
(5)x的取值范围为0≤x≤15.
(6)当x=5.5元时,每个月可获得最大利润,最大的月利润是2402.5元.
分析 (1)商品原售价为每件50元,每件商品的售价上涨x元,则每件商品的售价=原售价+上涨的钱数;
(2)每件商品的利润=每件商品的售价-进价;
(3)根据“售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件”列出代数式;
(4)根据“每个月的销售利润=每件商品的利润×销量”列出函数表达式;
(5)根据“每件售价不能高于65元”可得到x的取值范围;
(6)根据二次函数的性质即可解决问题.
解答 解:(1)商品原售价为每件50元,每件商品的售价上涨x元,则每件商品的售价为:50+x;
(2)每件商品的利润可以表示为:(50+x)-40=10+x;
(3)销量可以表示为:210-10x;
(4)每个月的销售利润为y=(10+x)(210-10x)=-10x2+110x+2100;
(5)由于每件售价不能高于65元,所以x的取值范围:0≤x≤15;
(6)y=-10x2+110x+2100=-10(x-5.5)2+2402.5,
所以当x=5.5元时,每个月可获得最大利润,最大的月利润是2402.5元.
故答案为:50+x;10+x;210-10x;-10x2+110x+2100;0≤x≤15;5.5;2402.5.
点评 此题主要考查了二次函数的应用以及二次函数的最值问题,根据每天的利润=一件的利润×销售量,建立函数关系式,借助二次函数解决实际问题是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
15.若xm+nym-1(xyn+1)2=x8y9,则4m-3n=( )
| A. | 10 | B. | 9 | ||
| C. | 8 | D. | 以上结果都不正确 |
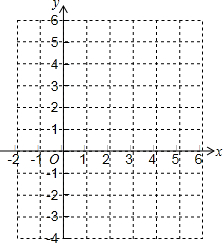 两个一次函数y=5-x和y=2x-1的图象交点的坐标与方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解有什么关系?
两个一次函数y=5-x和y=2x-1的图象交点的坐标与方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解有什么关系?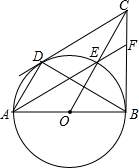 如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )