题目内容
7．先化简再求值$\frac{1}{a+1}$-$\frac{a+3}{{a}^{2}-1}$×$\frac{{a}^{2}-2a+1}{{a}^{2}+4a+3}$，已知a2+2a-7=0．分析 先根据题意得出a2+2a=7，再根据分式混合运算的法则把原式进行化简，把a2+2a=7代入进行计算即可．
解答 解：∵a2+2a-7=0，
∴a2+2a=7，
∴原式=$\frac{1}{a+1}$-$\frac{a+3}{（a+1）（a-1）}$•$\frac{（a-1）^{2}}{（a+1）（a+3）}$
=$\frac{1}{a+1}$-$\frac{a-1}{（a+1）^{2}}$
=$\frac{a+1-a+1}{{（a+1）}^{2}}$
=$\frac{2}{{（a+1）}^{2}}$
=$\frac{2}{{a}^{2}+2a+1}$，
当a2+2a=7时，原式=$\frac{2}{7+1}$=$\frac{1}{4}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
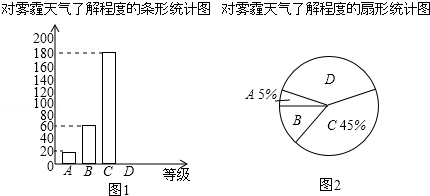
2．近几年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点．为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的三种统计图表．
对雾霾了解程度的统计表：
请结合统计图表，回答下列问题．
（1）本次参与调查的学生共有400人，m=15%，n=35%；
（2）图2所示的扇形统计图中D部分扇形所对应的圆心角是126度；
（3）请补全图1示数的条形统计图；
（4）根据调查结果，学校准备开展关于雾霾知识竞赛，某班要从“非常了解”态度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．
对雾霾了解程度的统计表：
| 对雾霾的了解程度 | 百分比 |
| A．非常了解 | 5% |
| B．比较了解 | m |
| C．基本了解 | 45% |
| D．不了解 | n |
（1）本次参与调查的学生共有400人，m=15%，n=35%；
（2）图2所示的扇形统计图中D部分扇形所对应的圆心角是126度；
（3）请补全图1示数的条形统计图；
（4）根据调查结果，学校准备开展关于雾霾知识竞赛，某班要从“非常了解”态度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．
16．
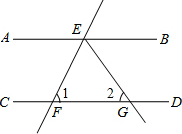如图，已知AB∥CD，直线EF分别交 AB、CD于点E，F，EG平分∠BEF交CD于点G．如果∠1=70°，那么∠2的度数是（ ）
如图，已知AB∥CD，直线EF分别交 AB、CD于点E，F，EG平分∠BEF交CD于点G．如果∠1=70°，那么∠2的度数是（ ）| A． | 70° | B． | 65° | C． | 55° | D． | 22.5° |