题目内容
12.若直线y=-2x+b经过点(3,5),则关于x的不等式-2x+b<5的解集是x>3.分析 根据直线y=-2x+b经过点(3,5),以及y随x的增大而减小即可求出关于x的不等式-2x+b<5的解集.
解答 解:∵直线y=-2x+b经过点(3,5),且k=-2<0,y随x的增大而减小,
∴关于x的不等式-2x+b<5的解集是x>3.
故答案为x>3.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
4.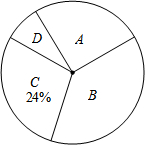 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
(1)表中的a=0.3b=6;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
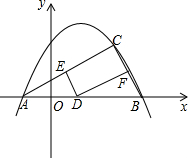 如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.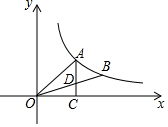 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.