题目内容
16. 如图,△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为( )
如图,△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为( )| A. | 3 | B. | $\frac{4}{3}$ | C. | 3或$\frac{4}{3}$ | D. | 4或$\frac{3}{4}$ |
分析 根据题目中的条件和三角形的相似,可以求得CE的长,本题得以解决.
解答 解:∵△DCE和△ABC相似,∠ACD=∠ABC,AC=6,AB=4,CD=2,
∴∠A=∠DCE,
∴$\frac{AB}{CD}$=$\frac{AC}{CE}$或$\frac{AB}{CE}$=$\frac{AC}{CD}$,
即$\frac{4}{2}$=$\frac{6}{CE}$或$\frac{4}{CE}$=$\frac{6}{2}$
解得,CE=3或CE=$\frac{4}{3}$
故选C.
点评 本题考查相似三角形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用三角形的相似解答.

练习册系列答案
相关题目
6.在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如表所示:
这些运动员跳高成绩的中位数和众数分别是( )
| 成绩(米) | 1.50 | 1.60 | 1.65 | 1.70 |
| 人数 | 1 | 2 | 3 | 4 |
| A. | 1.65,1.70 | B. | 1.65,1.65 | C. | 1.675,1.70 | D. | 1.625,1.70 |
7.下列各式中,是关于x,y的二元一次方程的是( )
| A. | 3x+y | B. | x-5y=12 | C. | 2xy+y-3=0 | D. | $\frac{5}{x}-y=1$ |
11.计算:$\sqrt{9}$=( )
| A. | 5 | B. | 2 | C. | 4 | D. | 3 |
1.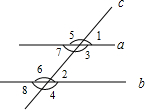 如图,直线a,b都与直线c相交,下列条件中:①∠1=∠2;②∠3=∠6;③∠5+∠7=180°;④∠5+∠8=180°,能判断a∥b的条件是( )
如图,直线a,b都与直线c相交,下列条件中:①∠1=∠2;②∠3=∠6;③∠5+∠7=180°;④∠5+∠8=180°,能判断a∥b的条件是( )
 如图,直线a,b都与直线c相交,下列条件中:①∠1=∠2;②∠3=∠6;③∠5+∠7=180°;④∠5+∠8=180°,能判断a∥b的条件是( )
如图,直线a,b都与直线c相交,下列条件中:①∠1=∠2;②∠3=∠6;③∠5+∠7=180°;④∠5+∠8=180°,能判断a∥b的条件是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
5.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$等于( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\overrightarrow{a}$-$\overrightarrow{b}$ |
6.下列运算正确的是( )
| A. | x3÷x2=x | B. | x3•x2=x6 | C. | x3-x2=x | D. | x3+x2=x5 |
 在图中,A(1,3),B(-2,0)和C(2,-4)是一个直角三角形的顶点.
在图中,A(1,3),B(-2,0)和C(2,-4)是一个直角三角形的顶点.