题目内容
 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合.下列结论中:
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合.下列结论中:①EF∥AB;②∠BAF=∠CAF;③S四边形ADFE=
| 1 |
| 2 |
正确的个数有( )
考点:翻折变换(折叠问题)
专题:
分析:根据翻折变换的性质可得AE=EF,AF⊥DE,∠ADE=∠EDF,∠AED=∠DEF,根据平行线的性质和等腰三角形三线合一的性质判断只有AB=AC时①②正确;根据对角线互相垂直的四边形的面积等于对角线乘积的一半可得S四边形ADFE=
AF•DE,判断出③正确;根据翻折的性质和平角的定义表示出∠ADE和∠AED,然后利用三角形的内角和定理列式整理即可得到∠BDF+∠FEC=2∠BAC,判断出④正确.
| 1 |
| 2 |
解答:解:∵△ABC沿DE折叠点A与BC边的中点F重合,
∴AE=EF,AF⊥DE,∠ADE=∠EDF,∠AED=∠DEF,
只有AB=AC时,∠BAF=∠CAF=∠AFE,
EF∥AB,故①②错误;
∵AF⊥DE,
∴S四边形ADFE=
AF•DE,故③正确;
由翻折的性质得,∠ADE=
(180°-∠BDF),∠AED=
(180°-∠FEC),
在△ADE中,∠ADE+∠AED+∠BAC=180°,
∴
(180°-∠BDF)+
(180°-∠FEC)+∠BAC=180°,
整理得,∠BDF+∠FEC=2∠BAC,故④正确.
综上所述,正确的是③④共2个.
故答案为:2.
∴AE=EF,AF⊥DE,∠ADE=∠EDF,∠AED=∠DEF,
只有AB=AC时,∠BAF=∠CAF=∠AFE,
EF∥AB,故①②错误;
∵AF⊥DE,
∴S四边形ADFE=
| 1 |
| 2 |
由翻折的性质得,∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
在△ADE中,∠ADE+∠AED+∠BAC=180°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
整理得,∠BDF+∠FEC=2∠BAC,故④正确.
综上所述,正确的是③④共2个.
故答案为:2.
点评:本题考查了翻折变换的性质,主要利用了平行线判定,等腰三角形三线合一的性质,三角形的内角和定理,熟记各性质并准确识图是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在CD上.
如图,AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在CD上. 如图,等腰直角三角形ABC直角边长为1,以它的斜边上的高AD为腰作第一个等腰直角三角形ADE;再以所作的第一个等腰直角三角形ADE的斜边上的高AF为腰作第二个等腰直角三角形AFG;…以此类推,这样所作的第n个等腰直角三角形的腰长为
如图,等腰直角三角形ABC直角边长为1,以它的斜边上的高AD为腰作第一个等腰直角三角形ADE;再以所作的第一个等腰直角三角形ADE的斜边上的高AF为腰作第二个等腰直角三角形AFG;…以此类推,这样所作的第n个等腰直角三角形的腰长为 如图,△ABC和△ADE都是等边三角形,∠DAC=14°,△ABD可以看成是△ACE绕点A顺时针旋转
如图,△ABC和△ADE都是等边三角形,∠DAC=14°,△ABD可以看成是△ACE绕点A顺时针旋转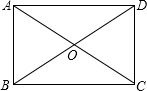 如图,矩形ABCD的对角线AC、BD的交点为O,已知BC=6cm,∠AOB=60°,则△BOC的面积为
如图,矩形ABCD的对角线AC、BD的交点为O,已知BC=6cm,∠AOB=60°,则△BOC的面积为