题目内容
2. 如图,△ABC的面积是12平分厘米,且AE=$\frac{1}{2}$EC,F是AD的中点,求图中阴影的面积.
如图,△ABC的面积是12平分厘米,且AE=$\frac{1}{2}$EC,F是AD的中点,求图中阴影的面积.
分析 连接CF,利用三角形面积与底的正比关系来推算得出结果即可.
解答 解:如图,
连接CF,
∵AE=$\frac{1}{2}$EC,所以S△ABE=$\frac{1}{3}$S△ABC=12×$\frac{1}{3}$=4(平方厘米),
S△EBC=$\frac{2}{3}$S△ABC.
又∵F是AD的中点,
∴S△ABF=S△FBD,S△AFC=S△DFC,
∴S△ABF+S△AFC=$\frac{1}{2}$×12=6(平方厘米).
∴S△EFC=(S△ABF+S△AFC)-S△ABE=6-4=2(平方厘米).
又∵S△AEF=$\frac{1}{2}$S△EFC=$\frac{1}{2}$×2=1(平方厘米).
S△DFC=S△AEF+S△EFC=1+2=3(平方厘米),
∴S阴影=S△EFC+S△DFC=2+3=5(平方厘米).
点评 此题考查学生对三角形的面积公式的运用掌握情况,以及分析图形的能力,掌握高相等的三角形,面积比等于底边的比是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
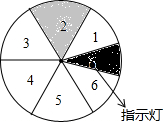 如图,将一个圆盘六等分,并把六个区域分别标上1,2,3,4,5,6,只有区域2为感应区域,中心角为30°的扇形AOB绕点O转动,在其半径OB上装有带指示灯的感应装置,当扇形AOB与区域2有重叠(O点除外)的部分时,指示灯会发光,否则不发光,当扇形ABO任意转动时,指示灯发光的概率为$\frac{1}{4}$.
如图,将一个圆盘六等分,并把六个区域分别标上1,2,3,4,5,6,只有区域2为感应区域,中心角为30°的扇形AOB绕点O转动,在其半径OB上装有带指示灯的感应装置,当扇形AOB与区域2有重叠(O点除外)的部分时,指示灯会发光,否则不发光,当扇形ABO任意转动时,指示灯发光的概率为$\frac{1}{4}$. 已知一次函数y=kx+b的图象如图所示
已知一次函数y=kx+b的图象如图所示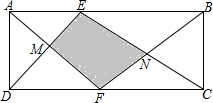 如图,长方形ABCD中,E、F分别是AB、DC上的点,AF、DE交于点M,BF、CE交于点N,若S△ADM=3cm2,S△BCN=4cm2,求阴影部分的面积.
如图,长方形ABCD中,E、F分别是AB、DC上的点,AF、DE交于点M,BF、CE交于点N,若S△ADM=3cm2,S△BCN=4cm2,求阴影部分的面积. 如图所示,△ABC中,AE,CD分别为△ABC的高,若AB=5cm,AE=4cm,CD=3cm,求BC的长.
如图所示,△ABC中,AE,CD分别为△ABC的高,若AB=5cm,AE=4cm,CD=3cm,求BC的长.