题目内容
1.已知抛物线y=x2-4x+3.(1)在平面直角坐标系中画出这条抛物线.
(2)求这条抛物线与x轴的交点坐标.
(3)当x取什么值时,y>0.
(4)当x取什么值时,y随x的增大而减小.
分析 (1)先求出抛物线的顶点坐标及与x轴的交点,在坐标系内画出函数图象即可;
(2)由(1)可得出结论;
(3)直接根据函数图象可得出结论;
(4)根据抛物线的对称轴可直接得出结论.
解答  解:(1)∵抛物线y=x2-4x+3=(x-2)2-1,
解:(1)∵抛物线y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,-1),与y轴的交点为(0,3).
∵令y=0,则x=1或x=3,
∴抛物线与x轴的交点为(1,0),(3,0),
∴函数图象如图;
(2)由(1)可知,抛物线与x轴交点(1,0),(3,0);
(3)由函数图象可知,当x<1或x>3时,y>0;
(4)由函数图象可知,当x≤2时,y随x的增大而减小.
点评 本题考查的是抛物线与x轴的交点,能根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
10.公路养护小组乘车沿东西公路巡视维护,某天早上从A地出发,晚上最后到达B处,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如表.(单位:km)
(1)收工时B地在A地的何方,相距多远?
(2)在第5次纪录时距A地最远.
(3)若每1km耗油0.3升,问共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
(2)在第5次纪录时距A地最远.
(3)若每1km耗油0.3升,问共耗油多少升?
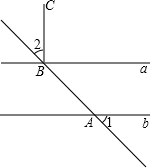 如图直线a∥b,直线c分别交直线a、b于点A、B两点,CB⊥b于点B,若∠1=60°,则∠2=30°.
如图直线a∥b,直线c分别交直线a、b于点A、B两点,CB⊥b于点B,若∠1=60°,则∠2=30°. 如图,AC=CD,AB=DE,CB=CE,∠ACB=80°,∠ACE=140°
如图,AC=CD,AB=DE,CB=CE,∠ACB=80°,∠ACE=140°