已知关于x.y的方程组$\left\{\begin{array}{l}3x+y=1+3a\\ x+3y=1-a\end{array}\right.$的解满足:x+y＞1.求a的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

1．已知关于x，y的方程组$\left\{\begin{array}{l}3x+y=1+3a\\ x+3y=1-a\end{array}\right.$的解满足：x+y＞1，求a的取值范围．

分析先把两式相加，再根据x+y＞1求出a的取值范围即可．

解答解：$\left\{\begin{array}{l}{3x+y=1+3a①}\\{x+3y=1-a②}\end{array}\right.$，①+②得，4（x+y）=2+2a，即x+y=$\frac{1}{2}$+$\frac{1}{2}$a，
∵x+y＞1，
∴$\frac{1}{2}$+$\frac{1}{2}$a＞1，解得a＞1．

点评本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．

练习册系列答案

相关题目

11．

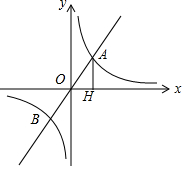已知：如图，正比例函数y=k₁x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B，点A在第一象限，且点A的横坐标为1，作AH垂直于x轴，垂足为点H，S_△AOH=1．
（1）求这两个函数的解析式；
（2）如果△OAC是以OA为腰的等腰三角形，且点C在x轴上，求点C的坐标．

12．下列数中能同时被2，5整除的最大的三位数是（　　）

9．若点A（a，b）在反比例函数y=$\frac{3}{x}$的图象上，则代数式ab-1的值为（　　）

16．

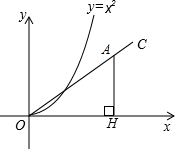如图，射线OC，与x轴的夹角为30^o，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x²（x＞0）上取点P，在y轴上取点Q，使得以P、O、Q为顶点的三角形与△AOH全等，则符合条件的点A的个数是（　　）

6．

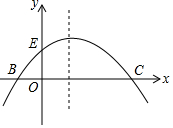如图，已知抛物线y=-$\frac{1}{m}$（x+2）（x-m）（其中m＞0）与x轴交于点B、C（点B在点C的左侧），与y轴交于点E．
（1）若该抛物线经过点M（4，2），求实数m的值和△BCE的面积．
（2）若该抛物线的对称轴上存在一点H，使得BH+EH的最小值为2$\sqrt{5}$，求此时点H的坐标．
（3）在第四象限内的抛物线上是否存在一点F，使得△BCF∽△BEC？若存在，求m的值；若不存在，请说明理由．

13．若二元一次方程组$\left\{\begin{array}{l}{2x+5y=-26}\\{ax-by=-4}\end{array}\right.$和$\left\{\begin{array}{l}{3x-5y=36}\\{bx+ay=-8}\end{array}\right.$有相同的解．求（2a+b）²⁰¹⁷的值．

10．解不等式-2x-1≥$\frac{-10x+1}{6}$．

3．若a=-$\frac{1}{2014}$，b=-$\frac{1}{2015}$，则a，b的大小关系是a＜b．

试题分类