��Ŀ����
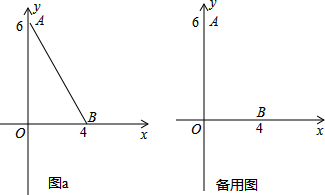
��ͼ��1����������ABCD�Ķ���B��C��˫����y=
�ϣ��������������������ϣ�
��1����OA=a��OD=b������ֱ��д��B��C�����꣨��a��b��ʾ����B�� �� ����C�� �� ����
����֤��a=b�� ���н��ۿ�ֱ���� ����
��2����ͼ��2������������BFGH����F��x���ϣ�H��˫�����ϣ���S������BFGH=5ʱ����k��
��3����ͼ��3����������BFGH����F��x���ϣ�H��˫�����ϣ�BH��BF=2��1����S����BFGH=17ʱ��
��ֱ��д��k��ֵ��

| k |
| x |
��1����OA=a��OD=b������ֱ��д��B��C�����꣨��a��b��ʾ����B��
����֤��a=b�� ���н��ۿ�ֱ���� ����
��2����ͼ��2������������BFGH����F��x���ϣ�H��˫�����ϣ���S������BFGH=5ʱ����k��
��3����ͼ��3����������BFGH����F��x���ϣ�H��˫�����ϣ�BH��BF=2��1����S����BFGH=17ʱ��
��ֱ��д��k��ֵ��

���㣺�����������ۺ���,ȫ�������ε��ж�������,���ɶ���,���ε�����,�����ε�����,���������ε��ж�������
ר�⣺�ۺ���
��������1���ٹ���C��CP��y���ڵ�P������B��BQ��x���ڵ�Q����ͼ��1������֤��CPD�ա�DOA����DOA�ա�AQB������PC=OD=AQ=b��PD=OA=BQ=a���Ϳɵõ�B��C�����ꣻ�ڰ�B��C�����������y=
������֤��a=b��
��2�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��2��������MF=a����FMB=��BNH=90�㣮��֤��BMF�ա�HNB������MF=NB=a���Ӷ��ɵõ�xHΪ3a���ٸ���B��H��˫����y=
�Ͽ����yH=
���Ӷ���NH=a-
=
����S������BFGH=5�����BH2=5����Rt��BNH�и��ݹ��ɶ��������a2=
���ɴ˿����k��ֵ��
��3�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��3��������MF=a����FMB=��BNH=90�㣮��֤��BMF�ס�HNB���������������ε����ʿɵ�NB=2MF=2a���Ӷ��õ�xHΪ4a������B��H��˫����y=
�Ͽɵ�yH=
������NH=a-
=
����S����BFGH=17�ɵ�BH2=34����Rt��BNH�и��ݹ��ɶ��������a2=8���ɴ˿����k��ֵ��
| k |
| x |
��2�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��2��������MF=a����FMB=��BNH=90�㣮��֤��BMF�ա�HNB������MF=NB=a���Ӷ��ɵõ�xHΪ3a���ٸ���B��H��˫����y=
| k |
| x |
| 2a |
| 3 |
| 2a |
| 3 |
| a |
| 3 |
| 9 |
| 2 |
��3�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��3��������MF=a����FMB=��BNH=90�㣮��֤��BMF�ס�HNB���������������ε����ʿɵ�NB=2MF=2a���Ӷ��õ�xHΪ4a������B��H��˫����y=
| k |
| x |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
����⣺��1����B��a+b��a����Cb��a+b����
����˼·������C��CP��y���ڵ�P������B��BQ��x���ڵ�Q����ͼ��1����

��֤��CPD�ա�DOA����DOA�ա�AQB������PC=OD=AQ=b��PD=OA=BQ=a��
����B��a+b��a����Cb��a+b����
�ʴ�Ϊ��a+b��a��b��a+b��
��֤������B��C��˫����y=
�ϣ�
��k=a��a+b��=b��a+b����
��a+b��0��
��a=b��
��2�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��2����

����MF=a����FMB=��BNH=90�㣮
���ı���BFGH�������Σ�
��BF=BH����FBH=90�㣬
���MBF=180��-90��-��NBH=90��-��NBH=��NHB��
�ڡ�BMF�͡�HNB�У�
��
���BMF�ա�HNB��SAS����
��MF=NB=a��
�ߵ�B������Ϊ��a+b��a������2a��a����
��xH=2a+a=3a��
��B��H��˫����y=
�ϣ�
��k=2a2=3a•yH��
��yH=
��
��NH=a-
=
��
��S������BFGH=5��
��BH2=5��
��Rt��BNH��
BH2=BN2+NH2=a2+��
��2=5��
��a2=
��
��k=2a2=9��
��3��k��ֵΪ16��
����˼·�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��3����

����MF=a����FMB=��BNH=90�㣮
��֤��BMF�ס�HNB��
��MF=a��BH��BF=2��1�ɵ�NB=2MF=2a��
��xH=2a+2a=4a��
��B��H��˫����y=
�Ͽɵ�yH=
��
����NH=a-
=
��
��S����BFGH=17�ɵ�BH2=34��
��Rt��BNH�и��ݹ��ɶ��������a2=8��
��k=2a2=16��
����˼·������C��CP��y���ڵ�P������B��BQ��x���ڵ�Q����ͼ��1����

��֤��CPD�ա�DOA����DOA�ա�AQB������PC=OD=AQ=b��PD=OA=BQ=a��
����B��a+b��a����Cb��a+b����
�ʴ�Ϊ��a+b��a��b��a+b��
��֤������B��C��˫����y=
| k |
| x |
��k=a��a+b��=b��a+b����
��a+b��0��
��a=b��
��2�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��2����

����MF=a����FMB=��BNH=90�㣮
���ı���BFGH�������Σ�
��BF=BH����FBH=90�㣬
���MBF=180��-90��-��NBH=90��-��NBH=��NHB��
�ڡ�BMF�͡�HNB�У�
|
���BMF�ա�HNB��SAS����
��MF=NB=a��
�ߵ�B������Ϊ��a+b��a������2a��a����
��xH=2a+a=3a��
��B��H��˫����y=
| k |
| x |
��k=2a2=3a•yH��
��yH=
| 2a |
| 3 |
��NH=a-
| 2a |
| 3 |
| a |
| 3 |
��S������BFGH=5��
��BH2=5��
��Rt��BNH��
BH2=BN2+NH2=a2+��
| a |
| 3 |
��a2=
| 9 |
| 2 |
��k=2a2=9��
��3��k��ֵΪ16��
����˼·�������Bƽ����x���ֱ�������Fƽ����y���ֱ�߽��ڵ�M�������Hƽ����y���ֱ�߽��ڵ�N����ͼ��3����

����MF=a����FMB=��BNH=90�㣮
��֤��BMF�ס�HNB��
��MF=a��BH��BF=2��1�ɵ�NB=2MF=2a��
��xH=2a+2a=4a��
��B��H��˫����y=
| k |
| x |
| a |
| 2 |
����NH=a-
| a |
| 2 |
| a |
| 2 |
��S����BFGH=17�ɵ�BH2=34��
��Rt��BNH�и��ݹ��ɶ��������a2=8��
��k=2a2=16��
������������Ҫ�����˷���������ͼ���ϵ������������ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ����������ε����ʡ����ε����ʵ�֪ʶ������K��ȫ�ȼ�K�������ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��A��-2��3������x��ĶԳƵ�A�������Ϊ��������
| A����2��-3�� |
| B����-2��-3�� |
| C����-2��3�� |
| D���� 2��3�� |
�����ĸ�ͼ�Σ�

��������Գ�ͼ�Σ��ҶԳ��������Ϊ2��ͼ�εĸ����ǣ�������

��������Գ�ͼ�Σ��ҶԳ��������Ϊ2��ͼ�εĸ����ǣ�������
| A��4 | B��3 | C��2 | D��1 |
���е�������Ҫ���ղ���ǣ�������
| A���˽�һ���ڵ������о��� |
| B������ȫ����ѧ����������� |
| C�����ij�����еĴ����� |
| D������ij��ũ����ij��� |
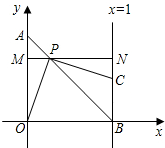 ��ͼ����OΪԭ���ֱ������ϵ�У�A�������Ϊ��0��1����ֱ��x=1��x���ڵ�B����Ϊ�߶�AB��һ���㣬��ֱ��PC��PO����ֱ��x=1�ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M����ֱ��x=1�ڵ�N����AP=x����PBC�����ΪS��
��ͼ����OΪԭ���ֱ������ϵ�У�A�������Ϊ��0��1����ֱ��x=1��x���ڵ�B����Ϊ�߶�AB��һ���㣬��ֱ��PC��PO����ֱ��x=1�ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M����ֱ��x=1�ڵ�N����AP=x����PBC�����ΪS��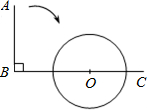 ��ͼ����ABC=90�㣬OΪ����BC��һ�㣬�Ե�OΪԲ�ģ�
��ͼ����ABC=90�㣬OΪ����BC��һ�㣬�Ե�OΪԲ�ģ�