Question

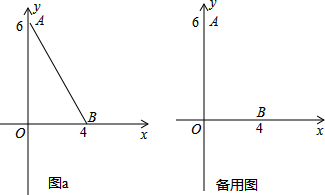
如图a，在平面直角坐标系中，A（0，6），B（4，0）
（1）按要求画图：在图a中，以原点O为位似中心，按比例尺1：2，将△AOB缩小，得到△DOC，使△AOB与△DOC在原点O的两侧，并写出点A的对应点D的坐标为

 

，点B的对应点C的坐标为

 

．
（2）在y轴上是否存在点M，使△OCM∽△ODC？若存在，请求出点M的坐标；若不存在，请说明理由：
（3）连接BD，若点P在线段CB上，从点C向点B以每秒1个单位运动，点Q在线段BD上，从点B向点D以每秒1个单位运动，若P、Q两点同时分别从点C、点B点出发，经过t秒，当t为何值时，△BPQ是等腰三角形？

Answer 1

考点：相似形综合题

专题：综合题,分类讨论

分析：（1）由题可得：OD=

1

2

OA=3，OC=

1

2

OB=2，点D在y轴的负半轴上，点C在x轴的负半轴上，由此就可求出点D、C的坐标；
（2）由于∠COM=∠DOC=90°，当

OC

OD

=

OM

OC

时，可得到△OCM∽△ODC，由此可求出OM的值，就可得到点M的坐标；
（3）△BPQ为等腰三角形有三种可能：①QP=QB，②BP=BQ，③PQ=PB，然后只需运用等腰三角形及相似三角形的性质就可解决问题．

解答：解：（1）∵A（0，6），B（4，0），
∴OA=6，OB=4．
由题可得：OD=

1

2

OA=3，OC=

1

2

OB=2，点D在y轴的负半轴上，点C在x轴的负半轴上，
∴点D的坐标为（0，-3），点C的坐标为（-2，0），如图a所示．

故答案为：（0，-3）、（-2，0）；

（2）在y轴上存在点M，使△OCM∽△ODC，如图b，

∵∠COM=∠DOC=90°，
∴当

OC

OD

=

OM

OC

即

2

3

=

OM

2

时，△OCM∽△ODC，
此时OM=

4

3

，
∴点M的坐标为（0，

4

3

）或（0，-

4

3

）；

（3）由题可得：BC=4-（-2）=6，BD=

OD2+OB2

=5，
CP=BQ=1×t=t，BP=BC-CP=6-t．
①若QP=QB，
过点Q作QG⊥BP于G，如图c①，

则∠BGQ=90°，BG=PG=

1

2

BP=3-

1

2

t．
∵∠GBQ=∠OBD，∠BGQ=∠BOD=90°，
∴△BGQ∽△BOD，
∴

BG

BO

=

BQ

BD

，
∴

3- 1 2 t

4

=

t

5

，
解得：t=

30

13

；
②若BP=BQ，
如图c②，

则有6-t=t，
解得：t=3；
③若PQ=PB，
过点P作PH⊥BD于H，如图c③，

则∠PHB=90°，BH=QH=

1

2

BQ=

1

2

t．
∵∠PBH=∠DBO，∠PHB=∠DOB=90°，
∴△BHP∽△BOD，
∴

BH

BO

=

BP

BD

，
∴

1 2 t

4

=

6-t

5

，
解得：t=

48

13

．
综上所述：当t为

30

13

或3或

48

13

时，△BPQ是等腰三角形．

点评：本题主要考查了相似三角形的判定与性质、位似变换、等腰三角形的性质、勾股定理等知识，运用分类讨论的思想是解决第（3）小题的关键．