题目内容
4.某城市规定:出租车起步价允许行驶的最远路程为3千米.超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了8千米,付了17元”;乙说:“我乘这种出租车走了18千米,付了35元”.(1)请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
(2)若某人乘这种出租车行驶了x千米,请写出付费w元与x的函数关系式.
分析 (1)根据不同的路程的付费不同,可得方程组,根据解方程组,可得答案;
(2)分类讨论:起步价,超过起步价部分的费用等于起步价加超过部分的费用,可得函数解析式.
解答 解:(1)设起步价为x元,超过3千米后,每千米的车费是y元,由题意,得
$\left\{\begin{array}{l}{x+(8-3)y=17}\\{x+(18-3)y=35}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=8}\\{y=1.8}\end{array}\right.$,
答:种出租车的起步价是8元,超过3千米后,每千米的车费是1.8元;
(2)当0<x≤3时,y=8;
当x>3时,w=1.8(x-3)+8,
即w=$\left\{\begin{array}{l}{8(0<x≤3)}\\{1.8x+2.6(x>3)}\end{array}\right.$.
点评 本题考查了分段函数,(1)根据题意找出两个等量关系列方程组是解题关键;(2)分类讨论是解题关键.

练习册系列答案
相关题目
13.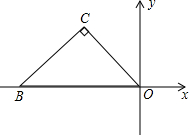 如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )
如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )
 如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )
如图,在直角坐标系中,△OBC的顶点O(0,0),B(-4,0),且∠0CB=90°,OC=BC,则点C关于y轴对称的点的坐标是( )| A. | (2,3) | B. | (2,2) | C. | (-2,-2) | D. | (2$\sqrt{2}$,2$\sqrt{2}$) |
15.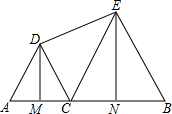 如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )
如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )
 如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )
如图,AB=2a,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着点A向点B的方向移动(不与点A、B重合),连接DE,得到四边形DMNE.这个四边形的面积为( )| A. | a2 | B. | $\frac{\sqrt{3}}{2}$a2 | C. | $\frac{\sqrt{3}}{4}$a2 | D. | 不能确定 |
 如图,以△ABC的顶点作半径为1的三个单位圆.则三个阴影部份面积的和等于$\frac{π}{2}$.
如图,以△ABC的顶点作半径为1的三个单位圆.则三个阴影部份面积的和等于$\frac{π}{2}$.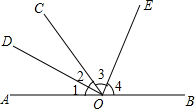 如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,OD⊥OE,垂足为点O.
如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,OD⊥OE,垂足为点O.