题目内容
20. 如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.
如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.(1)求证:AB∥DE;
(2)求EG的长.
分析 (1)由BE=CF,利用等式的性质得到BC=EF,利用SSS得到三角形ABC与三角形DEF全等,利用全等三角形对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证;
(2)由BE=CE得到E为BC中点,再由GE与AB平行,利用平行线等分线段定理得到G为AC中点,即GE为中位线,利用中位线定理得到AB=2EG,即可求出EG的长.
解答 解:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE;
(2)∵GE∥AB,E为BC中点,
∴G为AC中点,即GE为△ABC中位线,
∴EG=$\frac{1}{2}$AB=5.
点评 此题考查了全等三角形的判定与性质,以及平行线的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
10.甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.从甲、乙两箱中摸到黑球的概率分别用P甲、P乙表示,则( )
| A. | P甲>P乙 | B. | P甲<P乙 | ||
| C. | P甲=P乙 | D. | 无法比较P甲、P乙的大小 |
11.实数$\sqrt{3}-2$的绝对值是( )
| A. | $\sqrt{3}-2$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}+2$ | D. | 1 |
8.下列实数中属于无理数的是( )
| A. | 3.14 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{9}$ |
12.在Rt△ABC中,∠C=90°,BC=2,∠A=30°,则AC=( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{3}$ |
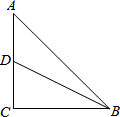 在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则:
在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则: 如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,交BC于点E,已知∠CAE=15°,AB=2cm,求∠BOE的度数及矩形ABCD的面积.
如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,交BC于点E,已知∠CAE=15°,AB=2cm,求∠BOE的度数及矩形ABCD的面积.