题目内容
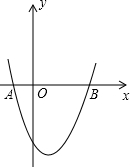 如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.考点:相似三角形的判定与性质,抛物线与x轴的交点
专题:
分析:当H点在C点上方时,当M在x轴上方时,连接CM交x轴于点E,由条件可证得AE=CE,可求得E点坐标,进一步可求得CE的解析式,联立两函数解析式可求得M点;当H在C点下方时,由条件可证明CM∥AB,可得出M点的坐标.
解答:解:令y=0,即x2-x-2=0,解得x=-1或x=2,
∴A(-1,0),C(0,-2),
∴AO=1,CO=2,
如图1,当H点在C点上方时,设直线CM交x轴于点E,

∵△CHM∽△AOC,
∴∠OAC=∠MCH,
∴EA=EC,
设E点坐标为(x,0),则OE=x,
∴AE=x+1,
在Rt△OCE中,OE=x,OC=2,由勾股定理可得CE=
,
∴x+1=
,
解得x=1.5,即E点坐标为(1.5,0),且C(0,-2),
设直线CE解析式为y=kx-2,把E点坐标代入可求得k=
,
∴直线CE解析式为y=
x-2,
联立两函数解析式可得
,解得
(舍去)或
,
此时M点坐标为(
,
);
如图2,当H点在C点下方时,

∵△CHM∽△AOC,
∴∠OAC=∠MCH,
又∵∠MCH=∠ACN,
∴∠MCH=∠OAC,
∴CM∥x轴
∴M点纵坐标为-2,代入y=x2-x-2可得x2-x=0,解得x=0(舍去)或x=1,
此时M点坐标为(1,-2);
综上可知,M点的坐标为(
,
)或(1,-2).
∴A(-1,0),C(0,-2),
∴AO=1,CO=2,
如图1,当H点在C点上方时,设直线CM交x轴于点E,

∵△CHM∽△AOC,
∴∠OAC=∠MCH,
∴EA=EC,
设E点坐标为(x,0),则OE=x,
∴AE=x+1,
在Rt△OCE中,OE=x,OC=2,由勾股定理可得CE=
| x2+4 |
∴x+1=
| x2+4 |
解得x=1.5,即E点坐标为(1.5,0),且C(0,-2),
设直线CE解析式为y=kx-2,把E点坐标代入可求得k=
| 4 |
| 3 |
∴直线CE解析式为y=
| 4 |
| 3 |
联立两函数解析式可得
|
|
|
此时M点坐标为(
| 7 |
| 3 |
| 22 |
| 3 |
如图2,当H点在C点下方时,

∵△CHM∽△AOC,
∴∠OAC=∠MCH,
又∵∠MCH=∠ACN,
∴∠MCH=∠OAC,
∴CM∥x轴
∴M点纵坐标为-2,代入y=x2-x-2可得x2-x=0,解得x=0(舍去)或x=1,
此时M点坐标为(1,-2);
综上可知,M点的坐标为(
| 7 |
| 3 |
| 22 |
| 3 |
点评:本题主要考查相似三角形的性质及等腰三角形的判定和性质、平行线的判定等知识的综合应用,掌握相似三角形对应角相等是解题的关键,注意分两种情况讨论及方程思想的应用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图所示,∠AOB=90°,OE、OC分别是∠AOD、∠DOB的角平分线,求∠COE的度数.
如图所示,∠AOB=90°,OE、OC分别是∠AOD、∠DOB的角平分线,求∠COE的度数. 如图是二次函数y=ax2+3x-a2+4的图象,则a的值为
如图是二次函数y=ax2+3x-a2+4的图象,则a的值为 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB=13米,它的坡角为45°,为了提高防洪能力,现将背水坡改造成坡比AC:DC=1:1.5的斜坡AD,求DB的长(结果精确到0.1m).
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB=13米,它的坡角为45°,为了提高防洪能力,现将背水坡改造成坡比AC:DC=1:1.5的斜坡AD,求DB的长(结果精确到0.1m).