题目内容
利用函数图象解下列方程.
(1)x2+x-6=0
(2)x2-x+3=0
(3)x2-8x+16=0.
(1)x2+x-6=0
(2)x2-x+3=0
(3)x2-8x+16=0.
考点:抛物线与x轴的交点
专题:
分析:根据题意画出函数y=x2+x-6①,y=x2-x+3②,y=x2-8x+16③的图象,根据函数图象与x轴的交点,得到对应方程的解.
解答: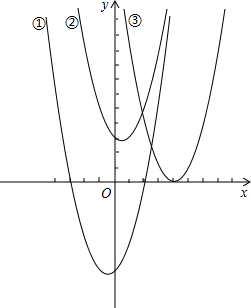 解:∵y=x2+x-6①,y=x2-x+3②,y=x2-8x+16③的图象如图所示,
解:∵y=x2+x-6①,y=x2-x+3②,y=x2-8x+16③的图象如图所示,
∴x2+x-6=0,x2-x+3=0,x2-8x+16=0的解得情况是:(1)x2+x-6=0有两个不相等的实数根:
x1=-3,x2=2;
(2)x2-x+3=0无实数根;
(3)x2-8x+16=0有两个相等的实数根x1=x2=4.
 解:∵y=x2+x-6①,y=x2-x+3②,y=x2-8x+16③的图象如图所示,
解:∵y=x2+x-6①,y=x2-x+3②,y=x2-8x+16③的图象如图所示,∴x2+x-6=0,x2-x+3=0,x2-8x+16=0的解得情况是:(1)x2+x-6=0有两个不相等的实数根:
x1=-3,x2=2;
(2)x2-x+3=0无实数根;
(3)x2-8x+16=0有两个相等的实数根x1=x2=4.
点评:本题考查了二次函数图象与一元二次方程的关系,画出图象,找到图象与x轴的交点是解题的关键.

练习册系列答案
相关题目
如果a<b<0,那么( )
| A、a2<b2 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,若DB⊥AE于B,DC⊥AF于C,延长BD交AF于点G,且DC=BD,∠ADG=120°,则下列结论正确的是:
如图,若DB⊥AE于B,DC⊥AF于C,延长BD交AF于点G,且DC=BD,∠ADG=120°,则下列结论正确的是: 如图所示是某长途汽车站旅客携带行李费用示意图.由图可知,行李的重量只要不超过
如图所示是某长途汽车站旅客携带行李费用示意图.由图可知,行李的重量只要不超过 如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由.
如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由.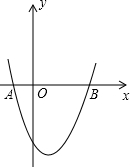 如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.