题目内容
在Rt△ABC中,∠C=90°,BC=8,tanB=
,求△ABC的周长和面积.
| 3 |
| 4 |
考点:解直角三角形
专题:
分析:根据tanB可以求得AC的值,即可求得△ABC面积,再根据勾股定理即可求得AB的值,即可求得△ABC的周长.
解答:解:∵Rt△ABC中,∠C=90°,BC=8,tanB=
,
∴AC=BC•tanB=6,
∴AB=
=10,
∴S△ABC=
×6×8=24,
△ABC周长=6+8+10=24.
答:△ABC的周长为24,面积为24.
| 3 |
| 4 |
∴AC=BC•tanB=6,
∴AB=
| BC2+AC2 |
∴S△ABC=
| 1 |
| 2 |
△ABC周长=6+8+10=24.
答:△ABC的周长为24,面积为24.
点评:本题考查了直角三角形中勾股定理的运用,考查了直角三角形面积的计算,考查了三角函数在直角三角形中运用,本题中求得AC的长是解题的关键.

练习册系列答案
相关题目
 如图所示,△ABC中,∠ACB>∠ABC,AE平分∠BAC,CD⊥AE于D,求证:∠ACD>∠B.
如图所示,△ABC中,∠ACB>∠ABC,AE平分∠BAC,CD⊥AE于D,求证:∠ACD>∠B. 如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由.
如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由. 如图,某人在A处测得大厦顶端B的仰角为30°,在点D处测得顶端B的仰角为45°.已知AD=20米,求大厦BC的高.
如图,某人在A处测得大厦顶端B的仰角为30°,在点D处测得顶端B的仰角为45°.已知AD=20米,求大厦BC的高.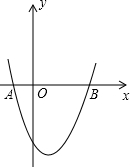 如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标. P从点B出发沿B-C-A以3厘米/秒的速度运动,点Q在从点C出发沿C-A-B运动,PQ两点同时运动,同时停止,运动时间为t秒.
P从点B出发沿B-C-A以3厘米/秒的速度运动,点Q在从点C出发沿C-A-B运动,PQ两点同时运动,同时停止,运动时间为t秒.