题目内容
 如图所示,∠AOB=90°,OE、OC分别是∠AOD、∠DOB的角平分线,求∠COE的度数.
如图所示,∠AOB=90°,OE、OC分别是∠AOD、∠DOB的角平分线,求∠COE的度数.考点:角平分线的定义
专题:
分析:直接根据角平分线的定义进行解答即可.
解答:解:∵OE、OC分别是∠AOD、∠DOB的角平分线,
∴∠EOD=
∠AOD,∠COD=
∠BOD.
∵∠AOB=90°,
∴∠COE=∠EOD+∠COD=
(∠AOD+∠BOD)=
∠AOB=
×90°=45°.
∴∠EOD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=90°,
∴∠COE=∠EOD+∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
点P在∠AOB的内部,下面个等式:①∠POA=∠BOP;②∠AOP=
∠AOB;③∠AOP=
∠BOP;④∠AOB=2∠BOP,其中能表示OP是∠AOB的角平分线的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如果a<b<0,那么( )
| A、a2<b2 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,若DB⊥AE于B,DC⊥AF于C,延长BD交AF于点G,且DC=BD,∠ADG=120°,则下列结论正确的是:
如图,若DB⊥AE于B,DC⊥AF于C,延长BD交AF于点G,且DC=BD,∠ADG=120°,则下列结论正确的是: 如图所示,△ABC中,∠ACB>∠ABC,AE平分∠BAC,CD⊥AE于D,求证:∠ACD>∠B.
如图所示,△ABC中,∠ACB>∠ABC,AE平分∠BAC,CD⊥AE于D,求证:∠ACD>∠B. 如图所示是某长途汽车站旅客携带行李费用示意图.由图可知,行李的重量只要不超过
如图所示是某长途汽车站旅客携带行李费用示意图.由图可知,行李的重量只要不超过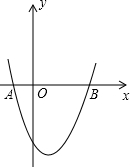 如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.