题目内容
 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB=13米,它的坡角为45°,为了提高防洪能力,现将背水坡改造成坡比AC:DC=1:1.5的斜坡AD,求DB的长(结果精确到0.1m).
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB=13米,它的坡角为45°,为了提高防洪能力,现将背水坡改造成坡比AC:DC=1:1.5的斜坡AD,求DB的长(结果精确到0.1m).考点:解直角三角形的应用-坡度坡角问题
专题:
分析:根据求DB的长,就要先求出CD和BC的长,也就是要先求出AC的长.直角三角形ACB中,有坡角的度数,有AB的长,易求得AC.
解答:解:在Rt△ABC中,∠ABC=45°.
则AC=AB•sin45°=13×
=
(米).
故BC=AC=
(米),
在Rt△ACD中,AD的坡比为1:1.5.
故AC:CD=1:1.5.
则CD=
(米),
故DB=DC-BC=
≈4.6(米).
答:DB的长为4.6m.
则AC=AB•sin45°=13×
| ||
| 2 |
| 13 |
| 2 |
| 2 |
故BC=AC=
| 13 |
| 2 |
| 2 |
在Rt△ACD中,AD的坡比为1:1.5.
故AC:CD=1:1.5.
则CD=
| 39 |
| 4 |
| 2 |
故DB=DC-BC=
| 13 |
| 4 |
| 2 |
答:DB的长为4.6m.
点评:此题主要考查了解直角三角形的应用,两个直角三角形有公共的直角边,先求出公共边是解决此类题目的基本出发点.

练习册系列答案
相关题目
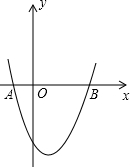 如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A,B两点,交y轴于C.过A、C画直线点M在抛物线上,过M作MH⊥AC,垂足为H.若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标.