题目内容
15.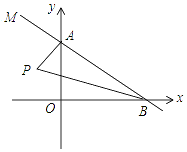 如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A、B两点,M在BA的延长线上,PA平分∠MAO,PB平分∠ABO,则∠P的度数是( )
如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A、B两点,M在BA的延长线上,PA平分∠MAO,PB平分∠ABO,则∠P的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
分析 由OA⊥OB即可得出∠OAB+∠ABO=90°、∠AOB=90°,再根据角平分线的定义以及三角形内角和定理即可求出∠P的度数.
解答 解:∵OA⊥OB,
∴∠OAB+∠ABO=90°,∠AOB=90°.
∵PA平分∠MAO,
∴∠PAO=$\frac{1}{2}$∠OAM=$\frac{1}{2}$(180°-∠OAB).
∵PB平分∠ABO,
∴∠ABP=$\frac{1}{2}$∠ABO,
∴∠P=180°-∠PAO-∠OAB-∠ABP=180°-$\frac{1}{2}$(180°-∠OAB)-∠OAB-$\frac{1}{2}$∠ABO=90°-$\frac{1}{2}$(∠OAB+∠ABO)=45°.
故选B.
点评 本题考查了三角形内角和定理,解题的关键是找出∠P=90°-$\frac{1}{2}$(∠OAB+∠ABO).本题属于基础题,难度不大,解决该题型题目时,熟练运用三角形内角和定理解决问题是关键

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3. 如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )
如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )
 如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )
如图,∠AOP=∠BOP,CP∥OB,CP=3,则OC=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.如果a-b=4,ab=7,那么a2b-ab2的值是( )
| A. | -28 | B. | -11 | C. | 28 | D. | 11 |
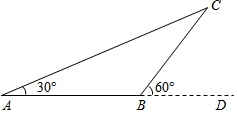 如图,小丽想知道自家门前小河的宽度,于是她测出如下数据:在河岸选取A点,A点对岸选取参照点C,测得∠A=30°;她沿河岸向前走了30米选取点B,并测得∠CBD=60°.根据数据能否测得小河宽度?若能请算出小河宽度,若不能请说明理由.
如图,小丽想知道自家门前小河的宽度,于是她测出如下数据:在河岸选取A点,A点对岸选取参照点C,测得∠A=30°;她沿河岸向前走了30米选取点B,并测得∠CBD=60°.根据数据能否测得小河宽度?若能请算出小河宽度,若不能请说明理由.