题目内容
 如图,OD是⊙O的半径,弦AB⊥OD于点C,连接BO并延长交⊙O于点E,连接EC,AE.若AB=8,CD=2,求CE的长.
如图,OD是⊙O的半径,弦AB⊥OD于点C,连接BO并延长交⊙O于点E,连接EC,AE.若AB=8,CD=2,求CE的长.考点:垂径定理,勾股定理,三角形中位线定理
专题:
分析:先根据垂径定理求出AC=BC,再设OB=r,则OC=r-CD=r-2,在△OBC中根据勾股定理求出r的值,进而得出OC的长,根据三角形中位线定理求出AE的长,由勾股定理即可得出结论.
解答:解:∵AB⊥OD,AB=8,
∴AC=BC=4,
设OB=r,则OC=r-CD=r-2,
在△OBC中,OB2=OC2+BC2,即r2=(r-2)2+42,解得r=5,
∴OC=5-2=3.
∵BE是⊙O的直径,
∵∠A=90°,
∴AE∥OD,
∵O是AB的中点,
∴OC是△ABE的中位线,
∴AE=2OC=6,
∴CE=
=
=2
.
∴AC=BC=4,
设OB=r,则OC=r-CD=r-2,
在△OBC中,OB2=OC2+BC2,即r2=(r-2)2+42,解得r=5,
∴OC=5-2=3.
∵BE是⊙O的直径,
∵∠A=90°,
∴AE∥OD,
∵O是AB的中点,
∴OC是△ABE的中位线,
∴AE=2OC=6,
∴CE=
| AE2+AC2 |
| 62+42 |
| 13 |
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
下列各题中的两个项,不属于同类项的是( )
A、
| ||
| B、1与-32 | ||
| C、a2b与5×102ba2 | ||
D、2x2y与-
|
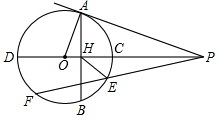 如图,已知⊙O的半径为3,AB为弦,CD是直径,AB⊥CD于点H,点P在DC的延长线上,且∠PAH=∠POA,OH:HC=1:2.
如图,已知⊙O的半径为3,AB为弦,CD是直径,AB⊥CD于点H,点P在DC的延长线上,且∠PAH=∠POA,OH:HC=1:2.
 如图所示,在⊙O中直径AB垂直于弦CD,垂足为E,若AB=10cm,CD=6cm,求OE的长.
如图所示,在⊙O中直径AB垂直于弦CD,垂足为E,若AB=10cm,CD=6cm,求OE的长. 在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)
在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)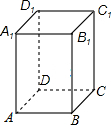 如图,有一个长、宽、高分别为2cm、2cm、3cm的长方体,有一只蚂蚁想沿着外侧壁从A点爬到C1处,请你帮助小蚂蚁计算出最短路线.
如图,有一个长、宽、高分别为2cm、2cm、3cm的长方体,有一只蚂蚁想沿着外侧壁从A点爬到C1处,请你帮助小蚂蚁计算出最短路线.