题目内容
 如图所示,已知在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,垂足为F,DB=DC.
如图所示,已知在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,垂足为F,DB=DC.求证:BE=CF.
考点:全等三角形的判定与性质
专题:证明题
分析:根据角平分线性质求出DE=DF,根据HL推出△BED≌△CFD即可.
解答:证明:∵在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,
∴DE=DF,∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
∴DE=DF,∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,
|
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
点评:本题考查了角平分线的性质和全等三角形的性质和判定的应用,解此题的关键是推出△BED≌△CFD,注意:全等三角形的对应边相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等边三角形的对称轴有( )
| A、1条 | B、1条或3条 |
| C、3条 | D、4条 |
 如图,每个小正方形的边长都等于1,则△ABC的外心坐标是
如图,每个小正方形的边长都等于1,则△ABC的外心坐标是 如图,半径为30cm的转动轮转过240°时,传送带上的物体A平移的距离为
如图,半径为30cm的转动轮转过240°时,传送带上的物体A平移的距离为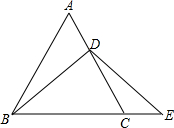 已知:△ABC是等边三角形,点D是线段AC上一点,作DB=ED,交BC延长线于点E.
已知:△ABC是等边三角形,点D是线段AC上一点,作DB=ED,交BC延长线于点E.