题目内容
3.已知,如图,以△ABC中的AB和AC为斜边,分别向△ABC的外侧作等腰直角三角形△ADB和等腰直角△AEC,M是BC的中点,过点D作DF⊥AB于F,连接FM.(1)如图1,若MF=3,求AC的长;(2)如图1,求证:MD=ME;
(3)如图2,在△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形△ADB和等腰直角△AEC,M是BC的中点,连接MD和ME,过点D作DE⊥AB于F,连接FM,猜想:△MDE是否是等腰直角三角形?若是,请证明;若不是,请说明理由.

分析 (1)根据三角形中位线定理即可解决.
(2)欲证明MD=ME只要证明△DFM≌△MGE即可.
(3)欲证明△EMD是等腰直角三角形,只要证明①EM=MD,可以通过△DFM≌△MGE进行证明,②∠EMD=90°,可以由∠OMD+∠MDO=90°来证明.
解答 (1)解:∵DF⊥AB,DB=DA,
∴AF=BF,
∵BM=MC,
∴FM=$\frac{1}{2}$AC即AC=2FM=6.
(2)证明:如图1中,取AC中点G,连接MG、EG.
∵△ADB、△AEC都是等腰直角三角形,AF=FB,AG=GC,
∴DF=AF=FB,GE=AG=GC,EG⊥AC,
∴∠DFB=∠EGC=90°,
∵AF=BF,BM=MC.AG=GC,
∴FM∥AG,MG∥AF
∴四边形AFGM是平行四边形,
∴FM=AG=GE,MG=AF=DF,∠BFM=∠BAC=∠CGM,
∵∠DFM=∠DFB+∠BFM,∠EGM=∠EGC+∠CGM,
∴∠DFM=∠EGM,
在△DFM和△MGE中,
$\left\{\begin{array}{l}{DF=MG}\\{∠DFM=∠MGE}\\{FM=GE}\end{array}\right.$,
∴△DFM≌△MGE,
∴DM=EM.
(3)△EMD是等腰直角三角形,理由如下,
证明:如图2中,取AC中点G,连接MG、EG,DF交MG于点O.
∵△ADB、△AEC都是等腰直角三角形,AF=FB,AG=GC,
∴DF=AF=FB,GE=AG=GC,EG⊥AC,
∴∠DFB=∠EGC=90°,
∵AF=BF,BM=MC.AG=GC,
∴FM∥AG,MG∥AF
∴四边形AFGM是平行四边形,
∴FM=AG=GE,MG=AF=DF,∠BFM=∠BAC=∠CGM,
∵∠DFM=∠DFB-∠BFM,∠EGM=∠EGC-∠CGM,
∴∠DFM=∠EGM,
在△DFM和△MGE中,
$\left\{\begin{array}{l}{DF=MG}\\{∠DFM=∠MGE}\\{FM=GE}\end{array}\right.$,
∴△DFM≌△MGE
∴DM=EM,∠MDF=∠EMG,
∵AB∥MG,
∴∠MOD=∠BFD=90°,
∴∠OMD+∠MDO=90°,
∴∠EMG+∠OMD=90°,
∴∠EMD=90°,
∴△EMD是等腰直角三角形.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的判定和性质等知识,添加辅助线构造全等三角形是解题关键,属于中考常考题型.

 ,若x=4,则y的值为( )
,若x=4,则y的值为( )| A. | 4 | B. | 10 | C. | 24 | D. | -4 |
| A. | 0 | B. | 1 | C. | 2 | D. | a取任何负数 |
 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 两点之间直线最短 | D. | 垂线段最短 |
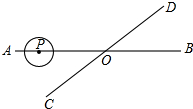 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.
如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切. 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.