题目内容
8.如图,在一张矩形纸片的一端,将折出的一个正方形展平后,又折成了两个相等的矩形,再把纸片展平,折出小矩形的对角线,并将小矩形的对角线折到原矩形的长边上.设MN的长为2,在下面给出的三种折叠中能得到长为($\sqrt{5}$-1)线段的有( )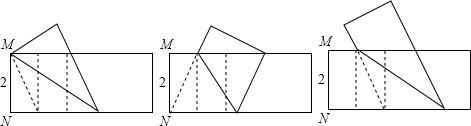
| A. | 0种 | B. | 1种 | C. | 2种 | D. | 3种 |
分析 利用勾股定理与折叠的性质逐一分析,得出对应线段的长度,进一步选择得出答案即可.
解答 解:如图: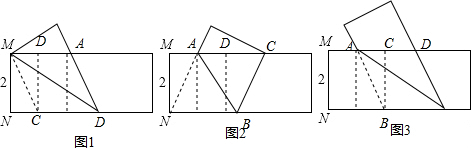
如图1,∵MN=2,则MD=1,
∴MC=$\sqrt{5}$,
∵折出内侧矩形的对角线MC,并把它折到图1中所示的AM处,
∴AM=MC=$\sqrt{5}$,
∴AD=$\sqrt{5}$-1;
如图2,∵MN=2,则AD=1,
∴AN=$\sqrt{5}$,
∵折出内侧矩形的对角线AN,并把它折到图3中所示的AC处,
∴AC=AN=$\sqrt{5}$,
∴CD=$\sqrt{5}$-1;
如图3,∵MN=2,则AC=1,BC=2,
∴AB=$\sqrt{5}$,
∵折出内侧矩形的对角线AB,并把它折到图3中所示的AD处,
∴AD=AB=$\sqrt{5}$,
∴CD=$\sqrt{5}$-1;
综上所知,三种折叠都能得到长为($\sqrt{5}$-1)线段.
故选:D.
点评 此题考查折叠的性质,勾股定理,利用折叠找出对应的边相等是解决问题的关键.

练习册系列答案
相关题目
17.a,b互为相反数,下列各数中,互为相反数的一组为( )
| A. | a2与b2 | B. | a3与b5 | ||
| C. | a2n与b2n (n为正整数) | D. | a2n+1与b2n+1 |
 如图,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F,AE=BF,则∠A=∠B吗?为什么?
如图,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F,AE=BF,则∠A=∠B吗?为什么?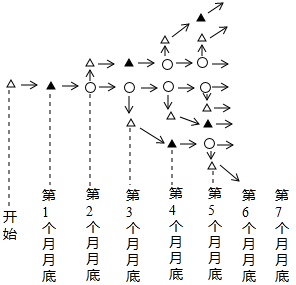 如果用△表示一对新出生的小兔,用▲表示一对一个月大的成年兔子,用○表示一对能生小兔的成年兔子,请你在图中标出第6个月月底和第7个月月底的各对兔子,把这幅图补充完整.
如果用△表示一对新出生的小兔,用▲表示一对一个月大的成年兔子,用○表示一对能生小兔的成年兔子,请你在图中标出第6个月月底和第7个月月底的各对兔子,把这幅图补充完整.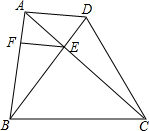 如图,已知在梯形ABCD中,AD∥BC,AC与BD交于点E,作EF∥BC交AB于点F,BC=CD,EF=ED.求证:△BCD是等边三角形.
如图,已知在梯形ABCD中,AD∥BC,AC与BD交于点E,作EF∥BC交AB于点F,BC=CD,EF=ED.求证:△BCD是等边三角形.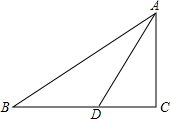 如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD=$\frac{10\sqrt{3}}{3}$cm,求∠B,AB,BC.
如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD=$\frac{10\sqrt{3}}{3}$cm,求∠B,AB,BC.