题目内容
5. 如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是6-π.
如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是6-π.
分析 分别求出DC=BC=CE=2,BD=BF=2$\sqrt{2}$,求出∠DCE=90°,∠DBF,分别求出△BCD、△BEF、扇形DBF、扇形DCE的面积,即可得出答案.
解答 解:
过F作FM⊥BE于M,则∠FME=∠FMB=90°,
∵四边形ABCD是正方形,AB=2,
∴∠DCB=90°,DC=BC=AB=2,∠DCB=45°,
由勾股定理得:BD=2$\sqrt{2}$,
∵将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,
∴∠DCE=90°,BF=BD=2$\sqrt{2}$,∠FBE=90°-45°=45°,
∴BM=FM=2,ME=2,
∴阴影部分的面积S=S△BCD+S△BFE+S扇形DCE-S扇形DBF
=$\frac{1}{2}×2×2$+$\frac{1}{2}×4×2$+$\frac{90π×{2}^{2}}{360}$-$\frac{90π×(2\sqrt{2})^{2}}{360}$
=6-π,
故答案为:6-π.
点评 本题考查了旋转的性质,解直角三角形,正方形的性质,扇形的面积计算等知识点,能求出各个部分的面积是解此题的关键.

练习册系列答案
相关题目
15.自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
| 使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
| 累计车费 | 0 | 0.5 | 0.9 | a | b | 1.5 |
| 使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
15.如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
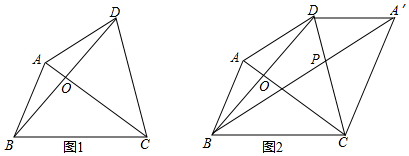
 如图,已知反比例函数y=$\frac{-3}{x}$与正比例函数y=kx(k<0)的图象相交于A、B两点,AC垂直x轴于C,则△ABC的面积为( )
如图,已知反比例函数y=$\frac{-3}{x}$与正比例函数y=kx(k<0)的图象相交于A、B两点,AC垂直x轴于C,则△ABC的面积为( )
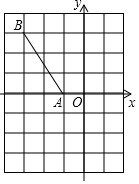 如图,线段AB的两个顶点都在方格纸的格点上,建立直角坐标系后点A的坐标是(-1,0),将线段AB绕点A顺时针旋转180°,则旋转后点B的对应点的坐标是(1,-3).
如图,线段AB的两个顶点都在方格纸的格点上,建立直角坐标系后点A的坐标是(-1,0),将线段AB绕点A顺时针旋转180°,则旋转后点B的对应点的坐标是(1,-3).