题目内容
10.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,带你C2在x轴上,将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2017的横坐标为12104.
分析 首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…每偶数之间的B相差12个单位长度,根据这个规律可以求得B2017的坐标.
解答 解:∵AO=3,BO=4,
∴AB=5,
∴OA+AB1+B1C2=3+5+4=12,
∴B2的横坐标为:12,且B2C2=4,
∴B4的横坐标为:2×12=24,
∵2017÷2=1008…1,
∴点B2017的横坐标为:1008×12+3+5=12104.
故答案为:12104.
点评 此题考查了点的坐标规律变换,通过图形旋转,找到所有B点之间的关系是本题的关键.题目难易程度适中,可以考查学生观察、发现问题的能力.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
1. 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )| A. | 14cm | B. | 11cm | C. | 6cm | D. | 3cm |
18.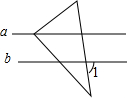 如图,直线a将三角板的直角分为相等的两个角,a∥b,则∠1的度数为( )
如图,直线a将三角板的直角分为相等的两个角,a∥b,则∠1的度数为( )
 如图,直线a将三角板的直角分为相等的两个角,a∥b,则∠1的度数为( )
如图,直线a将三角板的直角分为相等的两个角,a∥b,则∠1的度数为( )| A. | 70° | B. | 105° | C. | 60° | D. | 75° |
15. 为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )
为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )
 为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )
为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )| A. | $\left\{\begin{array}{l}{x+45y=180}\\{65x+y=10100}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{45x+y=180}\\{x+65y=10100}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=180}\\{65x+45y=10100}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{45x+65y=10100}\end{array}\right.$ |
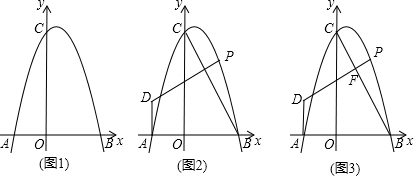
 如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是6-π.
如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是6-π.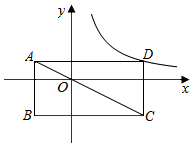 如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上.若点B的坐标为(-2,-2),则k=4.
如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上.若点B的坐标为(-2,-2),则k=4.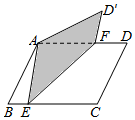 如图,?ABCD中,∠B=60°,AB=3,BC=4,折叠?ABCD使C落在A处,折痕为EF,点E、F分别在BC、AD上,则AF=$\frac{13}{5}$.
如图,?ABCD中,∠B=60°,AB=3,BC=4,折叠?ABCD使C落在A处,折痕为EF,点E、F分别在BC、AD上,则AF=$\frac{13}{5}$.