题目内容
15.已知一元二次方程(k-1)x2+kx+1=0有实数根,则k的取值范围是k≠1.分析 根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于k的不等式,解得即可,同时还应注意二次项系数不能为0.
解答 解:∵关于x的一元二次方程(k-1)x2+kx+1=0有实数根,
∴△=b2-4ac≥0,
即:k2-4(k-1)=(k-2)2≥0,
∴k全体实数,
∵k-1≠0,
∴k≠1,
∴k的取值范围是k≠1,
故答案为:k≠1.
点评 本题考查了根的判别式,解题的关键是了解根的判别式如何决定一元二次方程根的情况.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
4.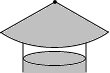 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )| A. | 288° | B. | 144° | C. | 216° | D. | 120° |
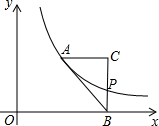 已知Rt△ABC(∠C=90°)是一块形状与大小均会发生变化的三角形纸板,在平面直角坐标系中,将△ABC按如图放置,AC∥x轴,点B在x轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象经过点A,与线段BC相交于点P,且A,P两点的横坐标分别为a,2a+2.
已知Rt△ABC(∠C=90°)是一块形状与大小均会发生变化的三角形纸板,在平面直角坐标系中,将△ABC按如图放置,AC∥x轴,点B在x轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象经过点A,与线段BC相交于点P,且A,P两点的横坐标分别为a,2a+2. 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.