题目内容
3.在△ABC中,若AB:BC:AC=3:4:5,则△ABC一定是( )| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 任意三角形 |
分析 根据勾股定理的逆定理求解即可.
解答 解:∵AB:BC:AC=3:4:5,
∴设AB=3x,则BC=4x,AC=5x,
∵(3x)2+(4x)2=(5x)2,
∴AB2+BC2=AC2,
∴△ABC为直角三角形.
故选C.
点评 本题考查勾股定理的逆定理,注意掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
13.下列调查适合普查的是( )
| A. | 调查2017年2月份利辛市场上某品牌饮料的质量 | |
| B. | 调查某月份长江安徽段水域的水质量情况 | |
| C. | 光明节能厂检测一批新型节能灯的使用寿命 | |
| D. | 了解某班50名学生的年龄情况 |
14.在平面直角坐标系中,点A的坐标为(1,2),将点A向右平移3个单位长度后得到A′,则点A′的坐标是( )
| A. | (-2,2) | B. | (1,5) | C. | (1,-1) | D. | (4,2) |
11.当x=2时,其值为零的分式是( )
| A. | $\frac{x-2}{{x}^{2}-3x+2}$ | B. | $\frac{1}{x-2}$ | C. | $\frac{2x-4}{x-1}$ | D. | $\frac{x+2}{x+1}$ |
8.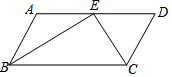 如图,平行四边形ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=5,CE=4,则AB的长是( )
如图,平行四边形ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=5,CE=4,则AB的长是( )
 如图,平行四边形ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=5,CE=4,则AB的长是( )
如图,平行四边形ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=5,CE=4,则AB的长是( )| A. | $\frac{{\sqrt{41}}}{2}$ | B. | 5 | C. | $\sqrt{29}$ | D. | 3 |
13.下列方程中,关于x的一元二次方程是( )
| A. | 3(x+1)2=2(x-1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2+2x=x2 |
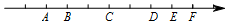 如图所示,一个单位长度表示1,观察图形,回答问题:
如图所示,一个单位长度表示1,观察图形,回答问题: