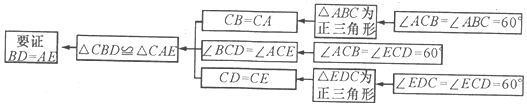
题目内容
17.问题:已知△ABC中,∠ABC=∠ACB=α,点D是AB边上任意一点,连结CD,在CD的上测作以CD为底边,α为底角的等腰△CDE,连结AE,试探究BD与AE的数量关系.(1)尝试探究
如图1,当α=60°时,小聪同学猜想有BD=AE,以下是他的思路呈现.请你根据他的思路把这个证明过程完整地表达出来;
(2)特例再探
如图2,当α=45°时,请你判断线段BD与AE之间的数量关系,并进行证明;
(3)问题解决
如图3,当α为任意锐角时,请直接写出线段BD与AE的数量关系是BD=2cosα•AE.(用含α的式子表示,其中0°<α<90°)
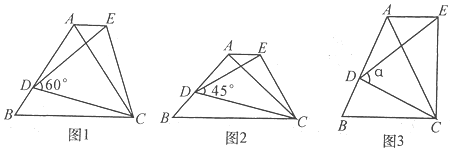
分析 (1)当α=60°时,△ABC、△DCE是等边三角形,连接EC,EC=DC,AC=BC,∠BCD=60°-∠ACD,∠ACE=60°-∠ACD,可得:△BDC≌△CAE(SAS),答案可证.
(2)过点D作DF∥AC,交BC于F,可证得△DFB是等腰直角三角形,BD=DF=$\frac{\sqrt{2}}{2}$BF,再证明△ADE∽△FCD,得:$\frac{AE}{DF}$=$\frac{AD}{CF}$.由DF∥AC,得:$\frac{BD}{BF}$=$\frac{AD}{CF}$可得到$\frac{AE}{BD}$=$\frac{BD}{BF}$=$\frac{\sqrt{2}}{2}$,继而得到答案.
(3)由连结EC,可利用四点共圆证角相等,然后证△BDC∽△AEC相似可以确定BD=2cosα•AE.
解答 解:(1)BD=AE;∵∠BCA=60°,∠DCE=60°,
∴∠BCD=∠ACE,
在△BDC与△AEC中,$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BDC≌△AEC,
∴BD=AE;
(2)BD=$\sqrt{2}$AE;理由如下:
过点D作DF∥AC,交BC于F.
∵DF∥AC,
∴∠ABC=∠DFB.
∵∠ABC=∠ACB=α,α=45°,
∴∠ABC=∠ACB=∠DFB=45°.
∴△DFB是等腰直角三角形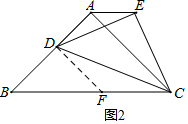
∴BD=DF=$\frac{\sqrt{2}}{2}$BF.
∵AE∥BC,
∴∠ABC+∠BAE=180°.
∵∠DFB+∠DFC=180°
∴∠BAE=∠DFC.
∵∠ABC+∠BCD=∠ADC,∠ABC=∠CDE=α,
∴∠ADE=∠BCD.
∴△ADE∽△FCD.
∴$\frac{AE}{DF}$=$\frac{AD}{CF}$.
∵DF∥AC,
∴$\frac{BD}{BF}$=$\frac{AD}{CF}$.
∴$\frac{AE}{BD}$=$\frac{BD}{BF}$=$\frac{\sqrt{2}}{2}$,
∴BD=$\sqrt{2}$AE.
(3)∵∠ABC=∠ACB=∠EDC=∠ECD=α,
∴∠BCD=∠ACE,
∵∠ADE+∠EDC=∠B+∠BCD,
∴∠ADE=∠ACE,
∴A、D、C、E四点共圆,
∴∠ADE=∠BCD=∠ACE,∠ABC=∠ACB=α,
∴△BDC∽△ACE,
∴$\frac{BD}{AE}$=$\frac{BC}{AC}$,
又∵$\frac{BC}{AC}$=cosα,
∴BD=2cosα•AE.
故答案为:BD=2cosα•AE.
点评 本题主要考查了等边三角形的性质以及三角形相似的判定与性质的综合应用,在解答本题时要注意类比思想的应用,正确绘图也是解题的关键.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案| A. | m≠1 | B. | m≥0 | C. | m≥0 且 m≠1 | D. | m为任意实数 |
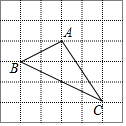 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$. 如图,已知BC∥DE,$\frac{AB}{AD}$=$\frac{3}{2}$,若BD=10cm,ED=6cm,求AD和BC的长度.
如图,已知BC∥DE,$\frac{AB}{AD}$=$\frac{3}{2}$,若BD=10cm,ED=6cm,求AD和BC的长度.