题目内容
4. 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4)、B(-4,n)两点.(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使∠APB是直角.
分析 (1)把点A(1,4)代入y=$\frac{k}{x}$即可求出k.
(2)把A(1,4)、B(-4,-1)两点代入y=kx+b求出k、b即可.
(3)设P(a,0)根据PM=$\frac{1}{2}$AB列出方程即可.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$经过点A(1,4)、B(-4,n),
∴m=4,n=-1,
∴反比例函数解析式为:y=$\frac{4}{x}$.
(2)∵一次函数y=kx+b经过点A(1,4)、B(-4,-1),
∴$\left\{\begin{array}{l}{k+b=4}\\{-4k+b=-1}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴一次函数为y=x+3.
(3)设P(a,0),AB点中点M(-$\frac{3}{2}$,$\frac{3}{2}$),
∵∠APB=90°,
∴PM=$\frac{1}{2}$AB,
∴$\sqrt{(a+\frac{3}{2})^{2}+(\frac{3}{2})^{2}}$=$\frac{1}{2}$×5$\sqrt{2}$,
整理得到:a2+3a-8=0解得a=$\frac{-3±\sqrt{41}}{2}$,
∴点P坐标为($\frac{-3+\sqrt{41}}{2}$,0)和($\frac{-3-\sqrt{41}}{2}$,0).
点评 本题考查一次函数、反比例函数的有关知识、直角三角形斜边中线的性质,解题的关键是会用待定系数法求函数解析式,用方程的思想去思考问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
 如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )| A. | 点M | B. | 点P | C. | 点Q | D. | 点N |
14.下列各项是同类项的是( )
| A. | 5与6 | B. | (a2)3与a5 | C. | 2a3与3a2 | D. | $\frac{1}{2}$m2n与-n2m |
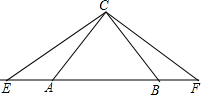 如图,已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=AC=2,求△ECF的面积.
如图,已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=AC=2,求△ECF的面积. 如图,扇形AOB的圆心角为60°,四边形OCDE是边长为1的菱形,点C、E、D分别在OA、OB和弧AB上,若过B作BF∥ED交CD的延长线于点F,则图中阴影部分的面积为$\frac{π-\sqrt{3}}{2}$.
如图,扇形AOB的圆心角为60°,四边形OCDE是边长为1的菱形,点C、E、D分别在OA、OB和弧AB上,若过B作BF∥ED交CD的延长线于点F,则图中阴影部分的面积为$\frac{π-\sqrt{3}}{2}$.