题目内容
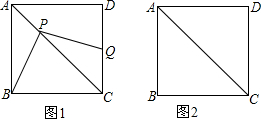
16. 如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2…,按此作法继续下去,则点A2014的纵坐标为($\frac{4}{3}$)2014.
如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2…,按此作法继续下去,则点A2014的纵坐标为($\frac{4}{3}$)2014.
分析 根据所给直线解析式可得l与x轴的夹角,进而根据所给条件依次得到点A1,A2的坐标,通过相应规律得到A2014坐标即可
解答  解:∵直线l的解析式为;y=$\sqrt{3}$x,
解:∵直线l的解析式为;y=$\sqrt{3}$x,
∴l与x轴的夹角为60°,
∵AB∥x轴,
∴∠ABO=60°,
∵OA=1,
∴OB=$\frac{OA}{sin60°}$=$\frac{2\sqrt{3}}{3}$,
∵A1B⊥l,
∴A1O=$\frac{OB}{cos30°}$=$\frac{4}{3}$,
∴A1(0,$\frac{4}{3}$),
同理可得A2(0,$\frac{16}{9}$),
…
∴A2014纵坐标为($\frac{4}{3}$)2014.
故答案为:($\frac{4}{3}$)2014.
点评 本题考查的是一次函数综合题,先根据所给一次函数判断出一次函数与x轴夹角是解决本题的突破点;根据含30°的直角三角形的特点依次得到A、A1、A2、A3…的点的坐标是解决本题的关键.

练习册系列答案
相关题目
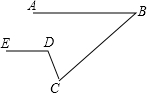 如图,已知AB∥DE,∠B=40°,∠EDC=110°,则∠C的度数为70°.
如图,已知AB∥DE,∠B=40°,∠EDC=110°,则∠C的度数为70°.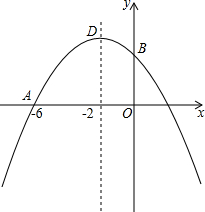 已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.
已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.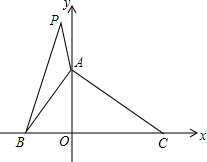 如图,已知在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
如图,已知在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).