Question

1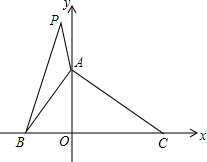．如图，已知在平面直角坐标系中，△ABO的面积为8，OA=OB，BC=12，点P的坐标是（a，6）．
（1）求△ABC三个顶点A，B，C的坐标；
（2）若点P坐标为（1，6），连接PA，PB，则△PAB的面积2；
（3）是否存在点P，使△PAB的面积等于△ABC的面积？如果存在，请求出点P的坐标．

Answer 1

分析 （1）根据三角形面积公式得到$\frac{1}{2}$•OA²=8，解得OA=4，则OB=OA=4，OC=BC-OB=8，然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标；
（2）利用S_△PAB=S_△PBH-S_△AOB-S_梯形AOHP求解；
（3）先计算出S_△ABC=24，分类讨论：当点P在第一象限，即a＞0，作PH⊥x轴于H，如图1，利用S_△PAB=S_△AOB+S_梯形AOHP-S_△PBH；当点P在第二象限，即a＜0，作PH⊥y轴于H，如图2，利用S_△PAB=S_梯形OHPB-S_△PAH-S_△OAB；分类得到2a-4=24或4-2a=24，然后分别求出a的值，从而确定P点坐标．

解答 解：（1）∵S_△ABO=$\frac{1}{2}$•OA•OB，
∵OA=OB，
∴$\frac{1}{2}$OA²=8，解得OA=4，
∴OB=OA=4，
∴OC=BC-OB=12-4=8，
∴A（0，4），B（-4，0），C（8，0）；
（2）作PH⊥x轴于H，如图1，
S_△PAB=S_△PBH-S_△AOB-S_梯形AOHP
=$\frac{1}{2}$×（4+1）×6-8-$\frac{1}{2}$×（4+6）×1
=15-8-5
=2．
（3）S_△ABC=$\frac{1}{2}$•4•12=24，
当点P在第一象限，即a＞0，作PH⊥x轴于H，如图2，
S_△PAB=S_△AOB+S_梯形AOHP-S_△PBH=8+$\frac{4+6}{2}$•a-$\frac{1}{2}$•6•（a+4）=2a-4；
则2a-4=24，
解得a=14．
此时P点坐标为（14，6）；
当点P在第二象限，即a＜0，作PH⊥y轴于H，如图3，
S_△PAB=S_梯形OHPB-S_△PAH-S_△OAB=$\frac{4-a}{2}$•6-$\frac{1}{2}$•（6-4）•a-8=4-2a；
则4-2a=24，
解得a=-10．
此时P点坐标为（-10，6）．
综上所述，点P的坐标为（-10，6）或（14，6）．

点评 本题考查了坐标与图形性质：利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系；记住三角形面积公式．