题目内容
7.直接写出下列各式中字母的取值范围:$\frac{{x}^{2}+3x-2}{2{x}^{2}+x}$:x≠0或x≠-$\frac{1}{2}$;$\frac{\sqrt{3-2x}}{x+1}$:x≤1.5且x≠-1.
分析 根据分式的意义,分母不等于0,可以求出x的范围.
根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:根据题意得:2x2+x≠0,
解得:x≠0或x≠-$\frac{1}{2}$.
根据题意得:3-2x≥0且x+1≠0,
解得:x≤1.5且x≠-1.
故答案为:x≠0或x≠-$\frac{1}{2}$;x≤1.5且x≠-1.
点评 考查了分式有意义的条件,二次根式有意义的条件,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
19.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
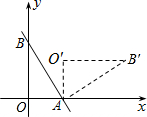 如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则直线AB′的函数解析式是y=0.5x-0.5.
如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则直线AB′的函数解析式是y=0.5x-0.5. 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PQ:QC=5:3:12.
如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PQ:QC=5:3:12.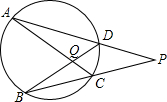 如图,直线PB、PA分别交圆于C、B,D、A,AC、BD交于Q,若$\widehat{AB}$:$\widehat{DC}$=3:1,∠AQB=α,求∠P.
如图,直线PB、PA分别交圆于C、B,D、A,AC、BD交于Q,若$\widehat{AB}$:$\widehat{DC}$=3:1,∠AQB=α,求∠P. 如图,正方形ABCD中,E是AB上的任意一点,∠ECF=45°,CF交AD于点F,将△CBE绕点C顺时针旋转到△CDG的位置.
如图,正方形ABCD中,E是AB上的任意一点,∠ECF=45°,CF交AD于点F,将△CBE绕点C顺时针旋转到△CDG的位置.