题目内容
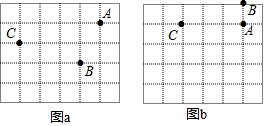
8.图a、图b是两张相同的方格纸,方格纸中的每个小正方形的边长均为1,点A、点B和点C在小正方形的顶点上,请在图a、图b中各画一个四边形,满足以下要求:(1)在图a中以AB和BC为边画一个面积为4的四边形ABCD,点D在小正方形的顶点上,且此四边形只有一组邻边相等;
(2)在图b中以AB和BC为边画一个周长为6+2$\sqrt{10}$的四边形ABCE,点E在小正方形的顶点上,且此四边形只有一组邻边相等.
分析 (1)根据勾股定理和三角形的面积公式,画出图形即可;
(2)根据勾股定理求出边长,画出图形即可.
解答  解:(1)如图1,
解:(1)如图1,
由勾股定理得:BC=DC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
四边形ABCD的面积=2×3÷2+2×1÷2=4;
(2)如图2,
由勾股定理得:BC=DC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,AD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
四边形ABCE的周长=6+2$\sqrt{10}$.
点评 本题考查了勾股定理、三角形面积公式、设计作图;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
18.|a|=a,则有理数a为( )
| A. | 正数 | B. | 负数 | C. | 正数和0 | D. | 负数和0 |
19.三角形的一边长是6,另外两边的长都是方程x2-19x+84=0的根,则该三角形的周长为( )
| A. | 14 | B. | 12 | C. | 12或14 | D. | 25 |
13.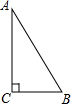 如图,Rt△ABC中,∠A=30°,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,∠A=30°,BC=2,AC=2$\sqrt{3}$,则AB长为( )
 如图,Rt△ABC中,∠A=30°,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,∠A=30°,BC=2,AC=2$\sqrt{3}$,则AB长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
18.平方根是$±\frac{1}{2}$的数是( )
| A. | $\frac{1}{4}$ | B. | $±\frac{1}{4}$ | C. | $±\sqrt{\frac{1}{2}}$ | D. | $\sqrt{\frac{1}{4}}$ |
 已知:a是-1,且a、b、c满足(c-6)2+|2a+b|=0,请回答问题:
已知:a是-1,且a、b、c满足(c-6)2+|2a+b|=0,请回答问题: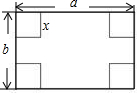 如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形,当a=12,x=3,且剪去部分的面积等于剩余部分的面积时,矩形的宽b为( )
如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形,当a=12,x=3,且剪去部分的面积等于剩余部分的面积时,矩形的宽b为( )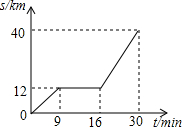 图中表示的是某汽车行驶的路程s(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
图中表示的是某汽车行驶的路程s(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题: