题目内容
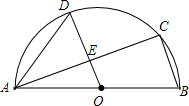 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.∠B=70°,求∠CAD的度数.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.∠B=70°,求∠CAD的度数.考点:圆周角定理
专题:
分析:根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得.
解答:解:∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°-∠B=90°-70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=
=
=55°
∴∠CAD=∠DAO-∠CAB=55°-20°=35°.
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°-∠B=90°-70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=
| 180°-∠AOD |
| 2 |
| 180°-70° |
| 2 |
∴∠CAD=∠DAO-∠CAB=55°-20°=35°.
点评:本题考查的是圆周角定理以及等腰三角形的性质,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
相关题目
已知Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中,正确的个数为( )
①所有的正三角形都相似;②所有的正方形都相似;③所有的等腰直角三角形都相似;④所有的矩形都相似.
①所有的正三角形都相似;②所有的正方形都相似;③所有的等腰直角三角形都相似;④所有的矩形都相似.
| A、1个 | B、2个 | C、3个 | D、4个 |
一个三角形的三边的比为2:3:4,则这个三角形三条边上的高的比为( )
| A、2:3:4 |
| B、6:4:3 |
| C、4:3:2 |
| D、4:9:6 |
一根1米长的小棒,第一次截去它的
,第二次截去剩下的
,第三次再截去剩下的
,如此截下去,第五次后剩下的小棒的长度是( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
A、(
| ||
B、[1-(
| ||
C、(
| ||
D、[1-(
|