题目内容
一个三角形的三边的比为2:3:4,则这个三角形三条边上的高的比为( )
| A、2:3:4 |
| B、6:4:3 |
| C、4:3:2 |
| D、4:9:6 |
考点:三角形的面积,比例的性质
专题:常规题型
分析:设首先设三角形三条边长分别为:2x、3x、4x,三边上高分别为a、b、c,根据三角形的面积公式可得
×2x•a=
×3x•b=
×4x•c,再算出a:b:c即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设三角形三条边长分别为:3x、4x、5x,三边上高分别为a、b、c,
×2x•a=
×3x•b=
×4x•c,
解得:a:b:c=6:4:3,
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:a:b:c=6:4:3,
故选:B.
点评:此题主要考查了三角形的面积公式,三角形的面积等于底边长与高线乘积的一半,即S△=
×底×高.
| 1 |
| 2 |

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,在⊙O中,∠BOC=120°,则∠BAC=( )
如图,在⊙O中,∠BOC=120°,则∠BAC=( )| A、120° | B、150° |
| C、60° | D、30° |
若(x2-y2)(x2-y2+1)=6,则x2-y2的值为( )
| A、2或-3 | B、2 |
| C、-3 | D、无数多个值 |
x2y3-5xy2-3次数和项数分别是( )
| A、5,3 | B、5,2 |
| C、2,3 | D、3,3 |
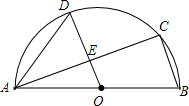 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.∠B=70°,求∠CAD的度数.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.∠B=70°,求∠CAD的度数.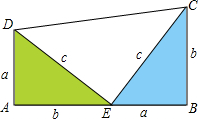 以a、b 为直角边(b>a),以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于
以a、b 为直角边(b>a),以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于