题目内容
10.因式分解:(1)x3-2x2y+xy2
(2)2x(m-n)-(n-m)
分析 (1)原式提取x,再利用完全平方公式分解即可;
(2)原式变形后,提取公因式即可.
解答 解:(1)原式=x(x2-2xy+y2)=x(x-y)2;
(2)原式=2x(m-n)+(m-n)=(m-n)(2x+1).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
2.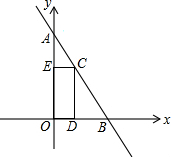 如图,一次函数y=-x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长( )
如图,一次函数y=-x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长( )
 如图,一次函数y=-x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长( )
如图,一次函数y=-x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长( )| A. | 逐渐变大 | B. | 不变 | C. | 逐渐变小 | D. | 先变小后变大 |
19. 如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
 如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )| A. | 50 | B. | 45 | C. | 40 | D. | 35 |
20.下列计算正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{9}$=±3 | C. | $\root{3}{-8}$=-2 | D. | $\sqrt{25}$-$\sqrt{16}$=$\sqrt{9}$ |
 已知直线y=2x+3与直线y=-2x-1.
已知直线y=2x+3与直线y=-2x-1.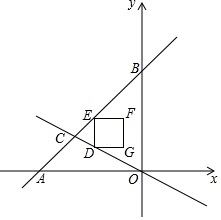 如图,直线y=x+6与x轴交于点A,与y轴交于点B,与直线y=-$\frac{1}{2}$x交于点C,D为线段OC上的动点,D与C,O不重合,作DE∥OB交AB于E,以DE为边在DE的右侧作正方形DEFO,正方形DEFG与△BOC重叠部分的面积为S,D点的横坐标为x,求S与x的函数关系式.
如图,直线y=x+6与x轴交于点A,与y轴交于点B,与直线y=-$\frac{1}{2}$x交于点C,D为线段OC上的动点,D与C,O不重合,作DE∥OB交AB于E,以DE为边在DE的右侧作正方形DEFO,正方形DEFG与△BOC重叠部分的面积为S,D点的横坐标为x,求S与x的函数关系式.