题目内容
1.$\sqrt{33}$的整数部分为m,小数部分为n,求n-$\frac{3}{2}$m.分析 先估算出$\sqrt{33}$的范围,求出m、n的值,再代入求出即可.
解答 解:∵25<33<36,
∴$5<\sqrt{33}<6$,
∴m=5
∴n=$\sqrt{33}-5$
∴$n-\frac{3}{2}m=\sqrt{33}-5-\frac{3}{2}×5=\sqrt{33}-\frac{25}{2}$.
点评 本题考查了估算无理数的大小和求代数式的值,能估算出$\sqrt{33}$的范围是解此题的关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
6.下列各式中,正确的是( )
| A. | $\sqrt{({-9)}^{2}}$=-9 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-27}$=-3 | D. | (-$\sqrt{2}$)2=-2 |
11.一辆汽车开往距离出发地180km目的地,出发后第一个小时按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地,设目前一小时的行驶速度为xkm/h,则所列方程正确的是( )
| A. | $\frac{180-x}{x}$-$\frac{180-x}{1.5x}$=40 | B. | $\frac{180-x}{x}$-$\frac{180-x}{1.5x}$=$\frac{40}{60}$ | ||
| C. | $\frac{180}{x}$-$\frac{180}{1.5x}$=40 | D. | $\frac{180}{x}$-$\frac{180}{1.5x}$=$\frac{40}{60}$ |
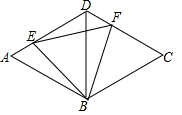 如图,在边长为4的菱形ABCD中,BD=4,E、F分别是边AD、CD上的动点,且AE+CF=4,连接BE、EF、FB.
如图,在边长为4的菱形ABCD中,BD=4,E、F分别是边AD、CD上的动点,且AE+CF=4,连接BE、EF、FB. 如图,若∠ADE=∠ABC,则DE∥BC,理由:同位角相等,两直线平行.
如图,若∠ADE=∠ABC,则DE∥BC,理由:同位角相等,两直线平行.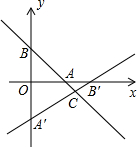 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴,y轴于点A,B,直线A′B′分别交x轴,y轴于点B′,A′,且△AOB≌△A′OB′.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴,y轴于点A,B,直线A′B′分别交x轴,y轴于点B′,A′,且△AOB≌△A′OB′.