题目内容
已知一组数据x1,x2,x3,…,xn的方差是s2,则一组新的数据:ax1+2,ax2+2,…,axn+2(a≠0,且为常数)的方差是 .
考点:方差
专题:计算题
分析:把数据:ax1+2,ax2+2,…,axn+2(a≠0,且为常数)都减去2得数据:ax1,ax2,…,axn(a≠0,且为常数),它们的方差不变,根据方差公式,当数据x1,x2,x3,…,xn的方差是s2时,数据:ax1,ax2,…,axn(a≠0,且为常数)的方差为a2s2.
解答:解:数据:ax1+2,ax2+2,…,axn+2(a≠0,且为常数)都减去2得数据:ax1,ax2,…,axn(a≠0,且为常数),
因为数据x1,x2,x3,…,xn的方差是s2,
所以数据:ax1,ax2,…,axn(a≠0,且为常数)的方差为a2s2.
故答案为a2s2.
因为数据x1,x2,x3,…,xn的方差是s2,
所以数据:ax1,ax2,…,axn(a≠0,且为常数)的方差为a2s2.
故答案为a2s2.
点评:本题考查了方差:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
 如图,将△ABC绕点O旋转,使顶点A与点A′重合,画出旋转后的图形.
如图,将△ABC绕点O旋转,使顶点A与点A′重合,画出旋转后的图形. 如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=4,则CF的长为( )
如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=4,则CF的长为( ) 如图,AB∥CD,CE平分∠ACD交AB于E点.
如图,AB∥CD,CE平分∠ACD交AB于E点.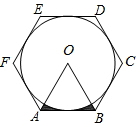 如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为
如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为