题目内容
 如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=4,则CF的长为( )
如图,△ABC中,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.EF=6,BE=4,则CF的长为( )| A、6 | B、4 | C、2 | D、5 |
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:如图,证明BE=OE,此为解题的关键性结论;证明CF=OF,即可解决问题.
解答: 解:如图,∵BO平分∠ABC,
解:如图,∵BO平分∠ABC,
∴∠ABO=∠CBO;
∵EO∥BC,
∴∠EOB=∠OBC,
∴∠EOB=∠EBO,
∴BE=OE;同理可证CF=OF;
∵EF=6,BE=4,
∴OF=EF-OE=EF-BE=2,
∴CF=OF=2,
故选C.
 解:如图,∵BO平分∠ABC,
解:如图,∵BO平分∠ABC,∴∠ABO=∠CBO;
∵EO∥BC,
∴∠EOB=∠OBC,
∴∠EOB=∠EBO,
∴BE=OE;同理可证CF=OF;
∵EF=6,BE=4,
∴OF=EF-OE=EF-BE=2,
∴CF=OF=2,
故选C.
点评:该题以三角形为载体,以考查等腰三角形的判定及其性质、平行线的性质等几何知识点为核心构造而成;牢固掌握等腰三角形的判定及其性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各数中,是负数的是( )
| A、0 | ||
| B、-1 | ||
C、
| ||
| D、2 |
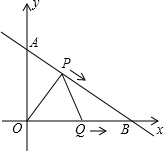 如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q分别为AB、OB边上的动点,它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒.设P、Q移动时间为t(0<t<4),解答下列问题:
如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q分别为AB、OB边上的动点,它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒.设P、Q移动时间为t(0<t<4),解答下列问题: 如图,直线PA是一次函数y=x+1的图象,直线PB经过(0,2)和(1,0)点.
如图,直线PA是一次函数y=x+1的图象,直线PB经过(0,2)和(1,0)点.