题目内容
 如图,AB∥CD,CE平分∠ACD交AB于E点.
如图,AB∥CD,CE平分∠ACD交AB于E点.(1)求证:△ACE是等腰三角形;
(2)若AC=13cm,CE=24cm,求△ACE的面积.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)如图,证明∠AEC=∠ACE,即可解决问题.
(2)如图,作辅助线;求出AG的长度,运用三角形的面积公式,即可解决问题.
(2)如图,作辅助线;求出AG的长度,运用三角形的面积公式,即可解决问题.
解答: (1)证明:如图,∵AB∥CD,
(1)证明:如图,∵AB∥CD,
∴∠AEC=∠DCE,
又∵CE平分∠ACD,
∴∠ACE=∠DCE,
∴∠AEC=∠ACE,
∴△ACE为等腰三角形.
(2)过A作AG⊥CE,垂足为G;
∵AC=AE,
∴CG=EG=
CE=12(cm);
∵AC=13(cm),
由勾股定理得,AG=5(cm);
∴S△ACE=
×24×5=60(cm2).
 (1)证明:如图,∵AB∥CD,
(1)证明:如图,∵AB∥CD,∴∠AEC=∠DCE,
又∵CE平分∠ACD,
∴∠ACE=∠DCE,
∴∠AEC=∠ACE,
∴△ACE为等腰三角形.
(2)过A作AG⊥CE,垂足为G;
∵AC=AE,
∴CG=EG=
| 1 |
| 2 |
∵AC=13(cm),
由勾股定理得,AG=5(cm);
∴S△ACE=
| 1 |
| 2 |
点评:该题主要考查了等腰三角形的判定及其性质的应用问题;解题的关键是牢固掌握等腰三角形的判定及其性质,这是灵活运用、解题的基础.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
下列各数中,是负数的是( )
| A、0 | ||
| B、-1 | ||
C、
| ||
| D、2 |
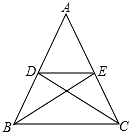 在等腰三角形ABC中,AB=AC,BE,CD分别是底角的平分线,DE∥BC,图中等腰三角形的个数有( )
在等腰三角形ABC中,AB=AC,BE,CD分别是底角的平分线,DE∥BC,图中等腰三角形的个数有( )| A、4个 | B、5个 | C、6个 | D、8个 |
 某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线是抛物线y=-x2+4x(单位:米)的一部分.则水喷出的最大高度是
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线是抛物线y=-x2+4x(单位:米)的一部分.则水喷出的最大高度是 如图,直线PA是一次函数y=x+1的图象,直线PB经过(0,2)和(1,0)点.
如图,直线PA是一次函数y=x+1的图象,直线PB经过(0,2)和(1,0)点. 若实数a,b在数轴上的位置如图所示,试把a,b,a-b,a+b按从小到大的顺序用“<”连接起来:
若实数a,b在数轴上的位置如图所示,试把a,b,a-b,a+b按从小到大的顺序用“<”连接起来: