题目内容
20. 如图,在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4…,则点A30的坐标是(-4$\sqrt{2}$,4$\sqrt{2}$).
如图,在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4…,则点A30的坐标是(-4$\sqrt{2}$,4$\sqrt{2}$).
分析 根据30÷4=7…2,得出A30在直线y=-x上,在第二象限,且在第8个圆上,求出OA30=8,通过解直角三角形即可求出答案.
解答 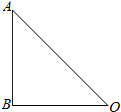 解:∵30÷4=7…2,
解:∵30÷4=7…2,
∴A30在直线y=-x上,且在第二象限,
即射线OA30与x轴的夹角是45°,如图OA=8,∠AOB=45°,
∵在直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,
∴OA30=8,
∵sin45°=$\frac{AB}{8}$,cos45°=$\frac{OB}{8}$,
∴AB=4$\sqrt{2}$,OB=4$\sqrt{2}$,
∵A30在第二象限
∴A30的横坐标是-8sin45°=-4$\sqrt{2}$,纵坐标是4$\sqrt{2}$,
即A30的坐标是:(-4$\sqrt{2}$,4$\sqrt{2}$).
故答案为:(-4$\sqrt{2}$,4$\sqrt{2}$).
点评 本题考查了解直角三角形,一次函数等知识点的应用,解此题的关键是确定出A30的位置(如在直线y=-x上、在第二象限、在第8个圆上),此题是一道比较好的题目,主要培养学生分析问题和解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.为了比较两箱樱桃的个头大小,分别在两箱樱桃中随机抽出若干颗樱桃,统计其质量(单位:g)如下表:
从樱桃的大小及匀称角度看,更好的一箱是甲箱.
表1:甲箱樱桃抽检结果
表2:乙箱樱桃的抽检结果
从樱桃的大小及匀称角度看,更好的一箱是甲箱.
表1:甲箱樱桃抽检结果
| 质量 | 8 | 9 | 10 | 11 | 12 |
| 颗数 | 0 | 3 | 5 | 3 | 1 |
| 质量 | 7 | 9 | 10 | 11 | 12 |
| 颗数 | 1 | 1 | 5 | 4 | 1 |
10.上周五股民新民买进某公司股票1 000股,每股35元,表为本周内每日股票的涨跌情况(单位:元):
则在星期五收盘时,每股的价格是34元.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
 如图,AB为⊙O的直径,C、E在⊙O上,∠BOE=20°,则∠ACE=100°.
如图,AB为⊙O的直径,C、E在⊙O上,∠BOE=20°,则∠ACE=100°. 如图所示的五角星图案绕着它的中心,至少旋转72度,能与其本身重合.
如图所示的五角星图案绕着它的中心,至少旋转72度,能与其本身重合.