Question

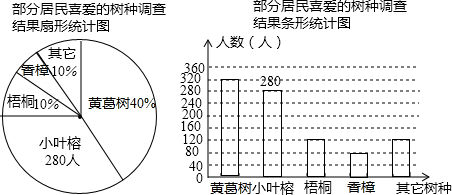
每年3月12日，是中国的植树节．某街道办事处为进一步改善人居环境，准备在街道两边植种行道树，行道树的树种选择取决于居民的喜爱情况．为此，街道办事处的人员随机调查了部分居民，并将结果绘制成如图中扇形统计图，其中∠AOB=126°．
请根据扇形统计图，完成下列问题：
（1）本次调查了多少名居民？其中喜爱香樟的居民有多少人？
（2）请将条形统计图补全（在图中完成）．
（3）某中学的一些同学也参与了投票，喜爱“小叶榕”的有四人，其中一名男生；喜爱“黄葛树”的也有四人，其中三名男生．若街道准备分别从这两组中随机选出一名同学参与到街道植树活动中去．请你用列表或画树状图的方法求出所选两名同学恰好是一名女生和一名男生的概率．

Answer 1

考点：列表法与树状图法,扇形统计图,条形统计图

专题：

分析：（1）根据小叶榕的圆心的角度求出所占的百分比，然后根据总人数等于喜欢小叶榕的人数除以所占的百分比，进行计算即可得解；再根据各部分所占的百分比的总和等于1求出喜欢香樟的居民所占的百分比，用总人数乘以喜欢香樟的居民所占的百分比，进行计算即可得解；
（2）根据总人数与各部分所占的百分比，求出喜欢香樟、梧桐、其它的人数，然后补全统计图即可；
（3）根据题意列表或树形图后即可求得概率．

解答：解：（1）“小叶榕”百分比：126÷360=0.35=35%，
共调查：280÷35%=800（人），
喜爱香樟的百分比为：1-35%-10%-10%-40%=1-95%=5%，
喜爱香樟的居民人数为：800×5%=40人；

（2）喜欢黄葛树的人数：800×40%=320人，
补全统计图如图；
由表可知，共有16中等可能的结果，其中是“一男一女”的结果有10种，
∴P（一男一女）=

10

16

=

5

8

；

（3）设男生为A，女生为B，列表得：

	A	A	A	B
A	AA	AA	AA	AB
B	BA	BA	BA	BB
B	BA	BA	BA	BB
B	BA	BA	BA	BB

点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．